Autor: Dr. Joan Nunes. Universitat Autònoma de Barcelona
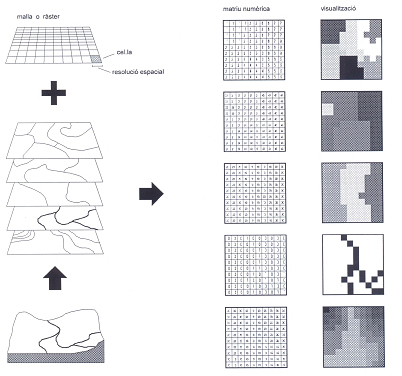
es basen totes en una mateixa estructura bàsica de representació de l'espai. L'espai a representar es subdivideix per mitjà d'una malla o quadrícula en un conjunt d'unitats elementals idèntiques ordenades de forma regular en files i columnes. Aquestes unitats elementals s'anomenen cel·les (o píxels en el cas de les imatges), ocupen una porció d'espai idèntica i regular, i reben com a valor el codi o valor numèric que expressa el valor de l'atribut representat per mitjà del ràster. En el cas de les imatges el valor numèric dels píxels expressa intensitat de llum o d'un dels components de color de la imatge. El conjunt de les cel·les forma el que s'anomena un ràster o una imatge digital.
El resultat de la representació ràster és equivalent al d'un mostreig espacial sistemàtic: un conjunt de valors mesurats en posicions separades per un interval de distància constant en les dues direccions, que poden anar referits al centre de la cel·la (per exemple, l'altitud) o bé al total de la superfície de la cel·la (per exemple, l'ús del sòl).
La forma més usual de les cel·les o píxels és el quadrat, resultant d'una malla quadrada regular, però hi ha altres formes possibles com per exemple el rectangle quan les dimensions de la cel·la (o la distància entre punts de mostreig) no són iguals en les dues direccions. El concepte de representació ràster mitjançant unitats superficials discretes com les tessel·les d'un mosaic ha estat generalitzat a altres formes d'unitats elementals, com és ara triangles, hexàgons o altres. En aquest sentit, es parla globalment de model de dades tessel·lar per a referir-se a tot tipus de representació de l'espai i estructura de dades resultant basada en particions de l'espai mitjançant una malla regular de qualsevol forma. El model de dades ràster es considera aleshores un cas particular del model de dades tessel·lar, el que es basa en malles quadrades o rectangulars. Els altres tipus de models tessel·lars, basats en malles d'altres formes, no han tingut, tanmateix, gaire acceptació ni aplicació per a la representació digital de la informació geoespacial.
El model de dades ràster és una representació de l'espai en dues dimensions. El concepte de cel·la o de píxel com a unitat quadrada elemental per a la representació discreta de l'espai en dues dimensions ha estat generalitzat al concepte de cub elemental, el vòxel, per a la representació discreta de l'espai en tres dimensions. L'estructura de dades basada en vòxels ha tingut una certa implementació en el programari de SIG tridimensional, però la major part de programari de SIG és encara bidimensional.
Sumari:
Origen
L'origen del model de dades ràster és el naixement de les imatges digitals i el desenvolupament posterior del processament digital d'imatges en els inicis de la informàtica gràfica. La primera imatge digital fou creada al National Bureau of Standards (actualment, National Institute of Standards and Technology, NIST) d'Estats Units l'any 1957 per mitjà del primer escàner de tambor. Durant la dècada de 1960 el processament digital d'imatges esdevindria un camp ben establert, gràcies al desenvolupament continuat de dispositius de captació d'imatges digitals i d'algorismes per al tractament de les imatges, amb aplicacions en l'exploració de l'espai, medicina i altres (Rosenfeld, 1969).
L'aplicació del model de dades ràster a l'enregistrament i anàlisi d'informació geoespacial data de la dècada de 1960 i d'entrada és força independent del desenvolupament del processament digital d'imatges. La principal motivació en aquest cas fou la necessitat de disposar d'una estructura de dades que permetés realitzar fàcilment les operacions d'anàlisi clàssiques de superposició de mapes (McHarg, 1969), o en general d'anàlisi cartogràfica, utilitzades en planificació del territori, arquitectura del paisatge i altres camps afins. En certa manera, aquest origen és simultani i paral·lel al del model vectorial en cartografia assistida per ordinador i en els primers sistemes d’informació geogràfica, de capacitat analítica limitada. Destaquen en aquest primer període els treballs desenvolupats al Laboratory for Computer Graphics and Spatial Analysis de Harvard University per part de Sinton i Steinitz (1969) per a crear diversos programes de sistemes d'informació geogràfica ràster, com és ara GRID i més endavant IMGRID (Sinton, 1977) o Map Analysis Package, MAP (Tomlin, 1985).
Representació ràster
En termes numèrics, un ràster té la mateixa estructura que una matriu numèrica: un conjunt de valors numèrics ordenats en files i columnes. La unitat espacial en un ràster, la cel·la, és fixa i per tant no cal emmagatzemar-ne la geometria, ja que es pot deduir de l'orientació i resolució de la malla. L'únic que s'emmagatzema en el cas d'un ràster o d'una imatge digital són els valors. Un ràster és, doncs, la simple llista ordenada dels valors, que els programes poden interpretar com a files successives de cel·les sabent el nombre de columnes i de files del ràster. En termes visuals, un ràster o imatge digital permet recrear una imatge analògica (visual) sobre el dispositiu de visualització (pantalla, impressora,...) gràcies a l'assignació d'un color a la regió de l'espai ocupada per cada cel·la en funció del valor de la cel·la. En termes espacials, tal com s'ha dit, un ràster o imatge digital és una partició regular de l'espai en unitats elementals, idèntiques en forma i extensió, ordenades de forma regular, com un mosaic.
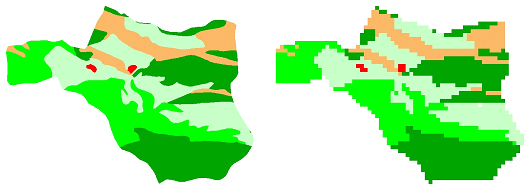
Un concepte crític pel que fa a la definició espacial dels ràsters i les imatges digitals és el de resolució espacial, que es defineix com la mida de les cel·les o píxels, i que en el cas més habitual de cel·les quadrades s'expressa per mitjà de la longitud del costat del quadrat que constitueix la cel·la. Com més petita la mida de les cel·les més alta és la resolució espacial del ràster (és a dir major capacitat de representació d'objectes petits i millor aproximació de les formes dels objectes); com és grans les cel·les, més baixa és la resolució espacial.
El caràcter discret de la representació ràster, combinat amb els efectes de la major o menor resolució, fan que la representació ràster dels diferents tipus d'elements geomètrics (punts, línies o polígons) prengui en els ràsters característiques particulars.
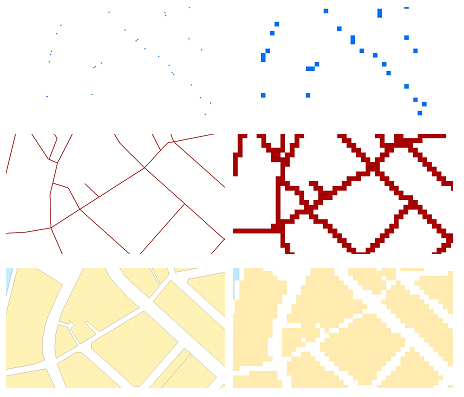
- els punts es representen en un ràster com a cel·les aïllades, de valor diferent que el de les cel·les del seu entorn.
- les línies es representen com un seguit de cel·les en contacte del mateix valor seguint una certa alineació.
- els polígons es representen en els ràsters com a conjunts de cel·les veïnes (taques) del mateix valor.
Cal tenir present, en qualsevol cas, que en realitat en un ràster només hi ha cel·les, totes iguals i independents. El reconeixement de punts, línies o polígons en un ràster és només una apreciació visual per part de l'observador (o el resultat de funcions de reconeixement d'objectes). Per tant no es pot parlar pròpiament de representació ràster de punts, línies o polígons, sinó de resultat de rasteritzar punts, línies o polígons.
En aquest sentit, a l'hora de rasteritzar informació vectorial d'elements geomètrics, hi ha diverses regles aplicables per a decidir quin valor assignar a cada cel·la per tal de representar els diversos elements. Algunes de les regles més emprades són:
- presència / absència: hom assigna a la cel·la un valor representatiu de l'element pel simple fet d'estar present dins la cel·la, independentment que ocupi poca o molta superfície o que l'element es trobi proper al centre de la cel·la. Emfatitza la presència dels elements i és útil per a rasteritzar punts o línies.
- centre de la cel·la: hom assigna a la cel·la el valor representatiu de l'element (o de l'absència d'elements) més proper al centre de la cel·la. Segueix el mateix criteri que els mostreigs regulars, en què es mesura el valor d'una variable en punts separats a intervals regulars i per tant en els centres de les àrees (cel·les) al seu entorn. Pot ser útil per a qualsevol tipus d'elements geomètrics i per als mostreigs pròpiament dits.
- àrea més gran: hom assigna a la cel·la el valor representatiu de l'element que ocupa una major superfície de la cel·la, és la regla mes habitual i útil per a rasteritzar polígons.
Geometria ràster
La geometria fixa d'un ràster fa innecessari haver d'emmagatzemar geometria i simplifica enormement les operacions espacials de càlcul. Alhora, la regularitat de la malla ràster proporciona una geometria alternativa basada en columnes i files.
En primer lloc, la pròpia malla del ràster queda completament definida pel nombre de columnes i de files i per la resolució espacial, que són els tres paràmetres que cal emmagatzemar, a més de la llista de valors corresponents a les cel·les. Aquests, i alguns altres, paràmetres no formen part de les dades en si, que estrictament són només els valors de les cel·les, sinó que formen la documentació o metadades que acompanyen necessàriament un conjunt de dades ràster perquè pugui ser interpretat correctament. Segons els formats de ràsters o d'imatges la documentació pot ser més o menys extensa i es pot incloure dins del mateix fitxer que els valors del ràster o imatge, típicament a la capçalera del fitxer, o bé anar en un o més fitxers a part.
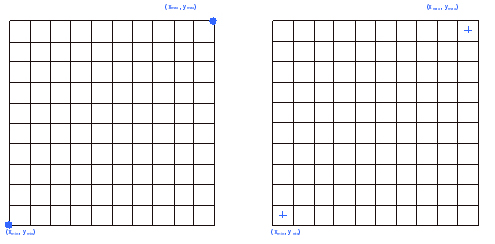
Per a georeferenciar el ràster i poder saber a quina posició geogràfica correspon cada cel·la, és suficient conèixer les coordenades georeferenciades (per exemple, UTM) d'un dels extrems de la malla. Generalment se sol emprar la cantonada de la cel·la de l'extrem inferior esquerre; és a dir, la x i y mínimes, sempre que el ràster o imatge sigui geomètricament correcte. En cas contrari, cal fer prèviament operacions de correcció geomètrica. Alguns formats ràster, o algunes maneres de documentar-los, donen, tanmateix, les coordenades georeferenciades del centre de la cel·la de l'extrem inferior esquerre en lloc de donar les de la cantonada d'aquesta cel·la, que és el més habitual. Altres formats o maneres de documentar, no gaire freqüents, donen com a referència les coordenades georeferenciades de la cantonada de la cel·la de l'extrem superior esquerre.
Generalment, a més de les coordenades de la cantonada inferior esquerra (x, y mínimes), es donen també les coordenades de la cantonada superior dreta (x, y màximes). Juntes, les coordenades mínimes i màximes, permeten conèixer l'extensió geogràfica del ràster o imatge.
Hi ha una relació fonamental entre l'extensió, la resolució espacial i el nombre de files i columnes d'un ràster, ja que coneguts dos d'aquests paràmetres el tercer queda determinat:
nombre de columnes = (xmax - xmin) / resolució espacial
nombre de files = (ymax - ymin) / resolució espacial
En cas de georeferenciar el ràster per mitjà de les coordenades dels centres, caldrà afegir una columna i una fila més al resultat de les expressions anteriors.
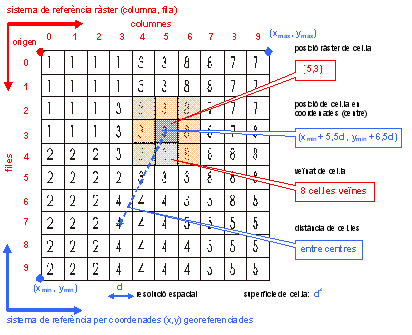
Les columnes i files d'un ràster donen lloc a un sistema de referència ràster que permet determinar la posició de cada cel·la (i identificar-la), indicant la columna i la fila en què es troba la cel·la. Aquest sistema de referència ràster té l'origen a l'extrem superior esquerre i augmenta d'esquerra a dreta (columnes) i de dalt a baix (files), contràriament a les coordenades rectangulars que tenen l'origen a l'extrem inferior esquerre i augmenten d'esquerra a dreta (x) i de baix a dalt (y). Generalment la numeració de columnes i files comença per 0.
La posició en coordenades georeferenciades d'una cel·la es dóna referida al centre de la cel·la i es calcula sabent les coordenades x, y mínimes, la posició en columnes i files de la cel·la i la resolució espacial.
L'entorn immediat d'una cel·la, format per les vuit cel·les veïnes al voltant de la cel·la, s'anomena el veïnat de la cel·la i intervé en moltes operacions d'anàlisi ràster, com per exemple el càlcul de la mitjana dels valors del veïnat, el càlcul de pendents o d'orientacions en el cas de l'altitud, etc. En algunes operacions més estrictes es pot distingir entre les cel·les veïnes que comparteixen costat (veïnat de torre), excloent les cel·les veïnes en diagonal, i el conjunt de les vuit cel·les veïnes (veïnat de dama). També és possible definir altres veïnats més amplis (per exemple, de 5 x 5 cel·les, de 7 x 7, o més).
La distància entre cel·les es calcula a partir dels centres de cel·la, mentre que la superfície en el cas de cel·les quadrades és el quadrat de la resolució espacial, de manera que per conèixer la superfície que ocupa un determinat valor en el ràster simplement cal comptar el nombre de cel·les d'aquest valor i multiplicar-ho per la superfície de la cel·la.
Estructures de dades ràster
L'estructura de dades ràster més senzilla és l'enumeració completa o llista dels valors de les cel·les. Aquesta estructura de dades resulta molt ineficient quan els valors de les cel·les es repeteixen sovint. En aquest sentit, hi ha un gran nombre d'estructures de dades que tenen per finalitat la compressió de les dades ràster. Cal fer notar, però, que en general es tracta de mètodes de compressió de l'emmagatzematge o formes d'emmagatzematge, que no alteren el model de dades en si. Entre aquests mètodes d'emmagatzematge, cal destacar
- codificació per cadenes: consisteix a descompondre el contorn d'un grup de cel·les de valor homogeni dins del ràster en una seqüència de vectors direccionals sobre la quadrícula, definits per la direcció i el nombre de cel·les que recorren. Per a cada regió s'emmagatzemen l'origen (fila i columna de la cel·la inicial), la seqüència de vectors que delimiten el contorn i el valor.
- codificació per longitud de recorregut (run-length encoding, RLE): descompon cada fila del ràster en grups de cel·les consecutives del mateix valor. Per a cada grup de cel·les consecutives del mateix valor, o recorregut, s'emmagatzema només el nombre de cel·les (longitud del recorregut) i el valor. Com que la codificació és seqüencial (per files i dins de cada fila), no cal emmagatzemar l'origen de cada grup. El mètode és efectiu a partir de 3 cel·les seguides del mateix valor, indiferent per a 2 i desfavorable per a 1 cel·la. Com més llarg és el recorregut, més eficient és la compressió. La codificació per longitud de recorregut és un dels mètodes més simples i més utilitzats per a la compressió d'emmagatzematge de dades ràster.
- codificació per blocs: consisteix a descompondre la malla original del ràster en blocs quadrats de valor homogeni i dimensió variable (n x n). Per a cada bloc s'emmagatzemen quatre dades: l'origen (fila i columna de la cel·la inferior esquerra), la longitud del costat del bloc (en nombre de cel·les) i el valor. L'emmagatzematge és eficient a partir de blocs de 3 x 3 cel·les, indiferent per a blocs de 2 x 2 i desfavorable per a 1 x 1. La codificació per blocs es pot convertir fàcilment a una codificació mitjançant arbres quaternaris.
- arbre quaternari: es basa en la subdivisió de l'espai representat en quadrants de valor homogeni de manera recursiva en un nombre variable de nivells, que poden arribar si cal a la cel·la individual, fins que es cobreix totalment l'element o grup de cel·les representat. El conjunt de quadrants formen un arbre jeràrquic amb un màxim de quatre nodes subsegüents per node i un mínim de zero si no té subdivisions. L'estructura d'arbre quaternari serveix per a codificar dades ràster categòriques i també per a indexar espacialment elements vectorials. El principal avantatge és la resolució variable, que permet que s'adapti a la disposició dels conjunts de cel·les contigües d'igual valor o a la forma dels elements vectorials. En el cas de les dades ràster estalvia espai d'emmagatzematge i supera les limitacions d'una resolució fixa. En el cas de les dades vectorials accelera la cerca dels elements. L'arbre quaternari és una estructura de dades espacials genuïna desenvolupada en el camp dels SIG que, a desgrat d'una notable popularitat com a estructura de codificació de dades ràster durant la dècada de 1980, actualment s'utilitza principalment com a mètode d'indexació espacial.
Més recentment, procedents del camp del processament digital d'imatges, s'han desenvolupat nombrosos formats de compressió d'imatges, entre els quals JPEG, GIF o MrSID, amb algorismes propis de compressió amb o sense degradació, que han esdevingut predominants com a formats d'emmagatzematge d'imatges i fins a cert punt també com a formats d'emmagatzematge de dades ràster.
Valors dels atributs en un ràster
Per la seva definició, els ràsters i les imatges solen representar només un atribut o característica mesurada, ja que la majoria de programes i de formats només permeten associar un valor a cada cel·la. També per definició, els valors de les cel·les dels ràsters i les imatges són sempre valors numèrics, amb independència que el seu significat siguin categories o realment quantitats. Això és degut al fet que els ràsters i les imatges digitals van ser concebuts, emmagatzemats i tractats inicialment com a matrius numèriques i aquestes només admeten un valor per posició.
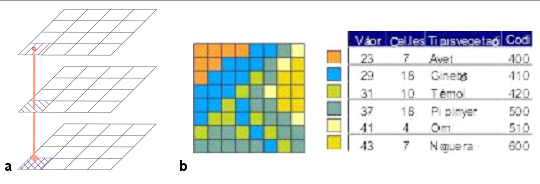
Generalment es necessita un ràster per a cada atribut mesurat. Per exemple, un per als usos del sòl, un altre per a l'altitud, etc. Així, en un sistema d'informació geogràfica (SIG), cada ràster correspon típicament a una capa del sistema d’informació geogràfica. Habitualment, les cel·les de totes les capes ràster són de la mateixa mida i posició, de manera que el conjunt de capes són un conjunt d'atributs mesurats sempre en les mateixes posicions fixes.
El fet d'enregistrar només un valor per a cada cel·la explica també que els ràsters no duguin generalment una taula associada per a emmagatzemar els atributs, ja que cada atribut requereix un ràster separat i els valors corresponents. Per aquesta raó no és gaire freqüent que els ràsters es puguin enllaçar amb bases de dades externes. Tot i això, hi ha excepcions i alguns formats de ràster inclouen a més del ràster en si una taula d'atributs dels valors. En aquests casos els valors numèrics del ràster serveixen de codis de classe i la taula d'atributs dels valors conté atributs associats a cada una de les classes representades pels valors del ràster. Per tant en aquests casos el ràster continua tenint també només un únic valor per cel·la i els atributs de la taula són funció de la classe i no atributs individuals per a cada cel·la. Sovint s'aprofita també aquesta taula per emmagatzemar el recompte del nombre de cel·les de cada valor, és a dir de cada classe.
Tipus de ràsters
Els termes ràster i imatge se solen utilitzar de forma diferenciada per referir-se a dos tipus de dades. El terme ràster sol referir-se a dades georeferenciades, que corresponen a una regió de l’espai geogràfic i en representen una característica o atribut, mesurada individualment per a cada cel·la, per exemple l’ús del sòl, l’altitud, la temperatura, etc. De vegades hom parla, respectivament, de ràsters temàtics i imatges.
El terme imatge digital, o simplement imatge, sol reservar-se per a qualsevol imatge captada per mitjà d’un dispositiu òptico-electrònic, ja sigui una imatge d’una regió de la superfície terrestre o d’una imatge qualsevol. En el primer cas, la imatge es podrà georeferenciar establint la posició geogràfica de cada cel·la per mitjà d’un sistema de referència espacial, mentre que en el cas d’una imatge qualsevol no tindria sentit (per exemple, la fotografia digital d’un vehicle, d'un objecte o d'una persona). Els valors de les cel.les de les imatges solen expressar per tant un valor d’intensitat lluminosa o de component de color, mesurat en una escala numèrica (típicament de 0 a 255). En el cas particular de les imatges de satèl·lit, el valor de les cel·les correspon a la intensitat de la radiació electromagnètica reflectida pels diferents materials de la superfície terrestre per a diverses longituds d’ona (és a dir tipus de llum) determinades.
A efectes de visualització i tractament és fonamental distingir diferents tipus de ràsters i d’imatges segons els tipus de valors de les cel·les o píxels. Així en el cas dels ràsters cal distingir entre:
- ràsters de valors categòrics: aquells en què els valors de les cel·les, encara que es tracti de valors numèrics, expressen atributs mesurats com a categories nominals (per exemple, usos del sòl) o ordinals (per exemple, risc d'incendi).
- ràsters de valors continus: aquells en què els valors de les cel·les expressen atributs mesurats realment com a quantitats en una escala contínua d'interval (per exemple, la temperatura) o de raó (per exemple, l'altitud).
Els ràsters de valors categòrics, segons el nombre de categories dels valors, es poden representar amb valors numèrics de tipus:
- bit: valors binaris (0,1), només dues categories.
- byte: valors de 0 a 255, en total 256 categories.
- enter: valors de -32768 a 32768, en total 65536 categories.
Els ràsters de valors continus solen representar-se amb valors numèrics de tipus real. També es poden representar per mitjà d'enters o d'un byte, si es prescindeix de decimals i es reescalen els valors originals al rang de valors admesos per aquests altres tipus de dades.
Les imatges, per la seva part, sempre presenten valors continus, ja que aquests expressen intensitats lluminoses o components de color, i per tant es mesuren sobre una escala numèrica contínua o aproximadament contínua, típicament de 0 a 255, ja que un byte per cel·la permet 256 valors diferents, que en molts casos és suficient. La diferenciació de les imatges sol respondre més aviat als següents casos:
- imatges d’una banda: aquelles que consten d’una sola imatge, distingint:
- imatges monocromes: un sol component de color per cel·la.
- imatges compostes pseudocolor: un sol valor per cel·la que expressa una determinada combinació de components de color.
- imatges multibanda: aquelles que consten de diverses imatges individuals, una per a cada longitud d’ona o component de color. Cada imatge individual (banda) d'una imatge multibanda es pot visualitzar individualment o de tres en tres (com a colors vermell, verd i blau, respectivament) formant composicions de color.
Visualització de ràsters
La visualització dels ràsters i de les imatges es duu a terme mitjançant l’assignació d’un color a cada cel·la (és a dir, a l’espai ocupat per cada cel·la) en funció del valor de la cel·la.
El mitjà per associar un color a cada valor és la paleta de colors, també anomenada color look-up table o colormap segons els programes.
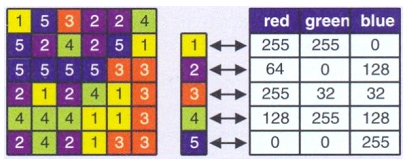
Una paleta de colors és simplement una taula en la qual s’indica per a cada valor possible de la imatge o ràster el color que li correspondrà en la visualització. Els colors s’expressen mitjançant algun sistema de colors, és a dir com a combinació dels diferents components que defineixen el sistema de colors emprat. El sistema de color més habitual és el sistema RGB, que descompon el color en els tres components additius vermell, verd i blau, típicament mesurats en una escala de 0 a 255. En el sistema RGB un color qualsevol s’expressa com una combinació de tres valors de 0 a 255, que indiquen respectivament la intensitat dels components vermell, verd i blau del color. Un format simple de paleta de color és un fitxer de text (o una taula) amb quatre columnes, la primera per a indicar els valors del ràster o imatge i les tres restants per a indicar, respectivament, els valors dels components vermell, verd i blau que formen el color assignat a cada valor.
A l’hora d’utilitzar i de crear paletes de color cal tenir en compte el tipus de valors del ràster o imatge a visualitzar i el rang d’aquests valors. Així, per a visualitzar un ràster de valors categòrics es necessita una paleta de colors categòrica, que permeti veure cada valor amb un color netament diferenciat de la resta. En aquest cas, a més, el rang de valors sol ser relativament petit, ja que el nombre de categories és limitat, i per tant és més que suficient una paleta de 256 colors i fins i tot de menys.
En el cas dels ràsters amb valors continus i de les imatges monocromes es necessita una paleta de colors contínua, en què els colors formin una gamma o gradació de color, de manera que la variació d’intensitat de l'atribut o de a magnitud representada a la imatge es pugui visualitzar com a variació gradual de color. Una paleta de colors típica per a valors continus és la que presenta una variació de tons de gris (escala de grisos) des del negre -corresponent al valor més baix a la imatge- fins al blanc -valor més alt present a la imatge-, si bé qualsevol gradació de colors pot resultar apropiada segons els casos. En cas que el rang dels valors superi el nombre de colors de la paleta de colors contínua (generalment 256), els programes reescalen automàticament els valors del ràster o imatge al rang 0-255 i els assignen el corresponent color de la paleta.
Molts programes són capaços de reconèixer automàticament el tipus de valors d'un ràster o d'una imatge, si més no el rang de valors, i apliquen automàticament una paleta de colors categòrica o contínua per defecte, que pot ser o no apropiada per a les necessitats de l'usuari. Altres programes demanen que se'ls indiqui explícitament la paleta de colors a aplicar. En general, una paleta de colors genèrica pot ser útil per a una visualització ràpida, però els millors efectes s'aconsegueixen amb paletes de colors personalitzades. Per exemple, una paleta de colors creada expressament per a simbolitzar els diferents tipus de vegetació amb colors apropiats.
Les imatges pseudocolor necessiten la paleta de colors pròpia de cada imatge, que es genera al mateix temps que la composició pseudocolor. Sovint aquesta paleta s’emmagatzema en el mateix fitxer, com en el cas dels formats TIFF o BMP, en què s’enregistren les imatges procedents d’escàners.
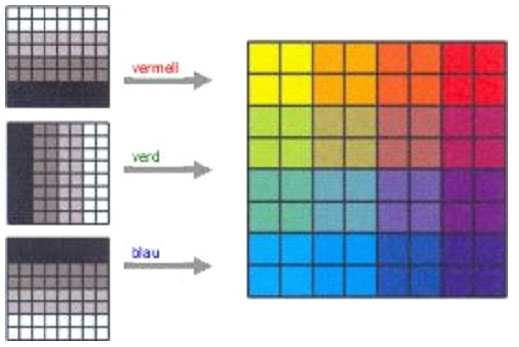
En el cas de les imatges multibanda, a part de visualitzar cada una de les imatges individuals (bandes) per separat com a imatges monocromes, és possible la visualització simultània de tres bandes formant el que es coneix pròpìament com a composició de color o composició de color RGB.
La visualització simultània de tres imatges en forma de composició de color és possible quan els valors originals de les imatges que intervenen en la composició estan compresos en el rang 0-255, de manera que es pot prendre el valor de cada una de les imatges individuals com el valor del component de color a què es faci correspondre la imatge. D’aquesta manera es prescindeix de la paleta de colors, ja que cada una de les tres imatges individuals expressa directament la intensitat del component de color corresponent, i per tant la combinació de valors de totes tres imatges per a cada cel·la determina el color amb què es veurà cada cel·la.
Generalment el sistema de color emprat per a la visualització en forma de composició de color és el sistema RGB i si, com és el cas de les imatges de satèl·lit, s’assigna a cada component del sistema RGB aquella imatge que representa la longitud d’ona corresponent a la llum del mateix color, s’obté el que s’anomena composició en color real. Qualsevol altra assignació diferent de regions de l’espectre electromagnètic -o, fins i tot, d’altres magnituds- als components de color RGB dóna lloc a una composició en fals color. Per exemple, assignat el canal infraroig proper al component vermell, el canal infraroig mitjà al component verd, i el canal vermell al component blau.
Tipus de dades geoespacials ràster
Segons el contingut d'informació els principals tipus de dades geoespacials ràster són els següents:
- imatges de satèl·lit
- fotografies aèries o ortofotomapes
- mapes escanejats
- ràsters temàtics, procedents de rasteritzar dades cartogràfiques vectorials o de classificar imatges aèries o de satèl·lit
- fotografies no territorials
Temes relacionats
- Georeferenciació
- Metadades geoespacials
- Model de dades vectorial
- Mostreig espacial
- SIG tridimensional
- Sistemes d’informació geogràfica
- Sistema de referència espacial
- Superposició
Referències
McHarg, I.L. (1969) Design with Nature, New York: Natural History Press.
Rosenfeld, A. (1969) Picture Processing by Computer, New York: Academic Press.
Sinton, D.F. and Steinitz, C.F. (1969) GRID: A user's manual, Cambridge, Massachussets: Laboratory for Computer Graphics and Spatial Analysis, Graduate School of Design, Harvard University.
Sinton, D.F. (1977) The user's guide to IMGRID: an information system for grid cell data structures, Cambridge, Massachussets: Department of Landscape Architecture, Graduate School of Design, Harvard University.
Tomlin, C.D. (1985) The IBM Personal Computer Version of the Map Analysis Package, Cambridge, Massachussets: Laboratory for Computer Graphics and Spatial Analysis, Graduate School of Design, Harvard University.
Lectures recomanades
Burrough, P.A. (1986) Principles of Geographical Information Systems for Land Resources Assessment, Oxford, UK, Clarendon Press. Chapter 2.
Lim, H. (2008) "Raster data" in Shekar, S. and Xiong, H. (eds.) Encyclopedia of GIS, New York: Springer.

 Contacte
Contacte