Autor: Dr. Joan Nunes. Universitat Autònoma de Barcelona
Promotor: Institut Cartogràfic de Catalunya, 2013
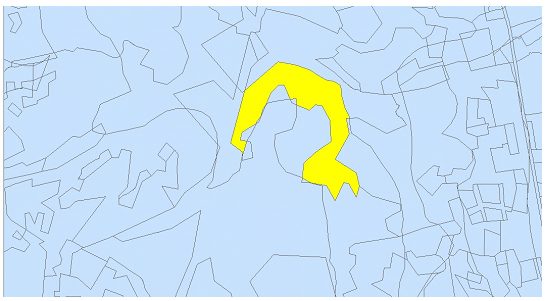
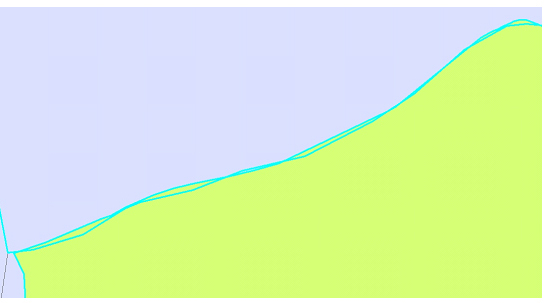
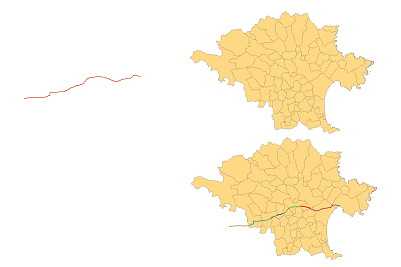
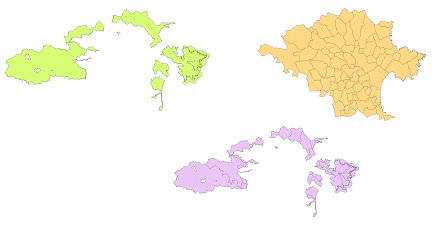
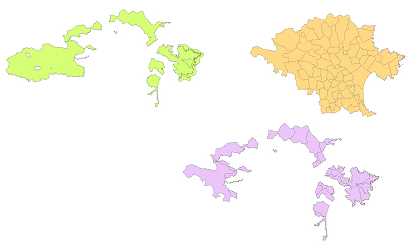
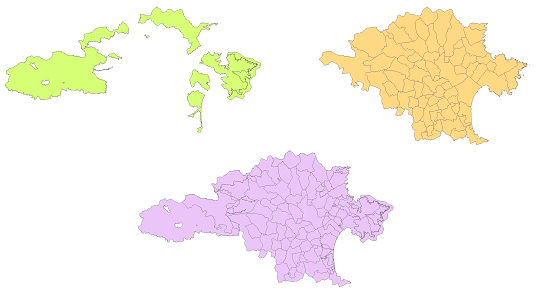
La superposició, també anomenada superposició de mapes o intersecció, és una operació espacial bàsica de geoprocessament en els sistemes d’informació geogràfica, que permet relacionar diferents conjunts de dades i quantificar l'abast de la relació d'encavalcament o coincidència parcial en l'espai entre diferents fenòmens representats en els diferents conjunts de dades.
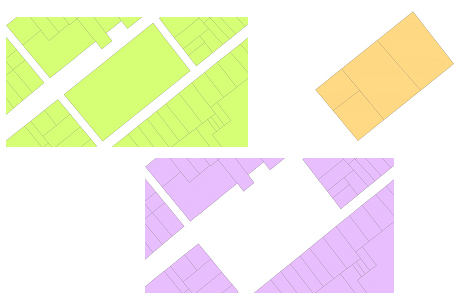
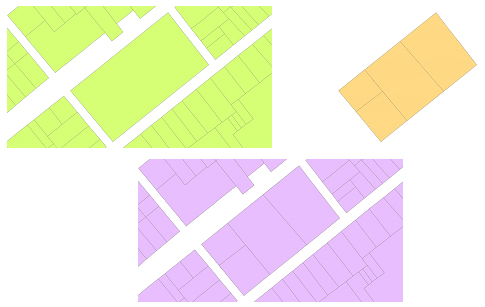
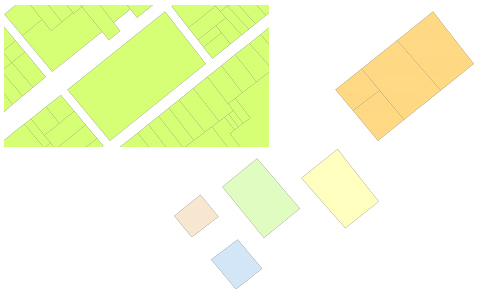
En el cas de la representació segons el model de dades vectorial, la superposició calcula la intersecció geomètrica dels elements pertanyents a diferents conjunts de dades i genera com a resultat un nou conjunt d'elements que són fragments dels elements originals dels diferents conjunts de dades superposats i n'hereten els atributs.
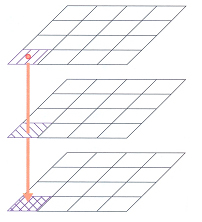
En el cas de la representació segons el model de dades ràster, la superposició opera els valors numèrics de les cel·les dels diferents conjunts de dades ràster, mitjançant operadors aritmètics o combinatoris, i produeix un nou conjunt de dades ràster que és conceptualment equivalent al resultat de la superposició vectorial.
La superposició constitueix la implementació digital de l'operació de superposició de mapes analògics sobre material transparent o amb taula de llum, clàssica en anàlisi cartogràfica i planificació.
Conceptualment, la superposició és una operació de desagregació de la informació geoespacial, que fragmenta els elements d'un conjunt de dades segons els elements d'un altre conjunt de dades per tal d'obtenir com es descomponen uns en funció dels altres i viceversa (per exemple, la superposició dels espais naturals i dels termes municipals permet dividir cada espai natural en les parts corresponents a cada un dels municipis). L'operació de superposició de mapes presenta també analogies amb l'encreuament de variables categòriques, atès que permet obtenir cada una de les combinacions de categories presents en l'espai cobert pels mapes superposats i quantificar posteriorment la freqüència i la superfícies de cada una de les combinacions presents. (per exemple, la superposició de les àrees d'usos del sòl i de litologia permet obtenir les àrees de cada combinació d'ús del sòl i tipus de roca). Igualment hi ha una forta analogia entre l'operació d'unió relacional de les bases de dades, que permet materialitzar la correspondència entre els individus de diferents entitats representades en taules, amb la superposició, que permet establir la correspondència en l'espai entre dos fenòmens qualssevol. De fet, la unió espacial és l'operació anàloga a la unió relacional, utilitzant condicions de relació espacial, i és un cas particular de superposició, en què no cal generar nous elements geomètrics per establir la correspondència. Finalment, i en última instància, la superposició és l'equivalent espacial de l'operador lògic AND i de la intersecció de conjunts.
L'operació de superposició no s'ha de confondre, òbviament, amb la superposició visual; és a dir, amb la visualització conjunta de diverses capes d'informació geogràfica d'una mateixa zona per a explorar-ne visualment les relacions, sense efectuar la intersecció geomètrica de les diverses capes.
Sumari:
- Origen
- Definició
- Operacions de superposició vectorial
3.1 Superposició segons la geometria dels elements
3.2 Superposició segons l'extensió geogràfica
3.3 Superposició segons el propòsit de la intersecció - Operacions de superposició ràster
4.1 Superposició ràster
4.2 Superposició ponderada - Temes relacionats
- Referències
- Lectures recomanades
Origen
La superposició és l'operació espacial per excel·lència dels sistemes d’informació geogràfica, contemplada en el programari de SIG vectorial des del principi (Tomlinson, 1967; 1980; Tomlinson et al., 1976). Igualment, les operacions ràster equivalents són també de les primeres operacions implementades en el programari de SIG ràster (Sinton and Steinitz, 1969; Tomlin, 1980). De fet, fins a finals de la dècada de 1980, la superposició ha estat considerada l'operació distintiva dels sistemes d’informació geogràfica, el que els atorgava capacitat d'anàlisi i, en última instància, el criteri per a decidir si un programa determinat es podia considerar o no un programa de SIG (Cowen, 1988)o bé tan sols un programa de cartografia assistida per ordinador.
L'operació de superposició dels sistemes d’informació geogràfica té el seu antecedent directe en l'operació manual de superposició de mapes analògics traçats sobre material transparent o opacs sobre una taula de llum, utilitzada a bastament en aplicacions de planificació, d'urbanisme, d'arquitectura del paisatge i de gestió forestal o de recursos naturals (McHarg, 1969), tot i la laboriositat d'haver de dibuixar manualment el mapa de les unitats intersecades a partir de la superposició dels mapes de les unitats originals.
Definició
La superposició genera nous elements geomètrics mitjançant la intersecció dels elements geomètrics de dos o més conjunts de dades. La superposició és un procés intensiu de càlcul, ja que la intersecció de dos conjunts d'elements geomètrics representats vectorialment implica calcular les interseccions entre tots els segments de recta que defineixen cada un dels elements geomètrics de cada conjunt de dades, per després construir els nous elements a partir de les línies resultants de la intersecció (White, 1990).
En el cas de conjunts de dades segons el model vectorial topològic la superposició ha d'aplicar el procés d'estructuració topològica a fi de generar la nova topologia arc-node resultant dels nous arcs obtinguts de la intersecció i, si es tracta d'una superposició de polígons, ha de construir els nous polígons resultat de la intersecció a partir de la nova topologia arc-node generada.
En el cas de conjunts de dades segons el model vectorial sense topologia, la intersecció de les línies (o dels contorns dels polígons) dels dos conjunts de dades originals dóna lloc directament a les noves línies (o als nous polígons). El procés pot ser relativament complex en cas que intervinguin elements multipart. Utilitzar l'estructura topològica com a auxiliar del procés d'intersecció, encara que els elements després s'emmagatzemin com elements simples, és una opció utilitzada en diversos algorismes de superposició. En aquest sentit, la definició del model de dades vectorial topològic (Peucker and Chrisman, 1975) va representar un dels avenços crítics per fer possible la intersecció massiva, ràpida i fiable, de conjunts de línies o de polígons (White, 1977).
Igual que en el procés d'estructuració topològica, en la superposició s'apliquen tots els mètodes per a reduir el nombre d'interseccions a calcular i accelerar el procés, com és ara la comparació de rectangles envoltants mínims, l'ordenació dels rectangles envoltants mínims en ordre decreixent de la coordenada y a fi de separar i processar els elements per bandes, i d'altres.
En la superposició també s'aplica, com en l'estructuració topològica, una tolerància de correcció a fi d'ajustar petites desviacions entre les coordenades de vèrtexs homòlegs en elements dels dos conjunts de dades. Això no obstant, és molt freqüent que en el procés de superposició es generi micropolígons al llarg de les vores dels polígons genuïns després de la superposició de dos conjunts de polígons, com a conseqüència d'un mal ajust entre els límits homòlegs dels polígons d'ambdós conjunts de dades. Els micropolígons constitueixen un error difícil de resoldre completament, ja que els criteris de superfície i de forma emprats en els procediments automàtics d'eliminació de micropolígons no aconsegueixen distingir del tot entre micropolígons i polígons genuïns. En el cas de la superposició, se'n pot prevenir l'aparició aplicant, durant la creació de les dades, el criteri de reproduir exactament les línies coincidents entre polígons de diferents conjunts de dades (per exemple, parcel·lari i usos del sòl). Amb tot, els micropolígons són inevitables fins a cert punt en la superposició de conjunts de polígons de temàtiques molt diferents (per exemple, vegetació i litologia).
Un cop generats els nous elements, el procés de superposició ha de transferir els atributs dels elements originals als elements resultat de la intersecció de manera que cada element nou hereti els atributs dels elements originals dels quals deriva. Aquest requeriment en el resultat obliga a mantenir durant tots el passos previs de càlcul d'interseccions, estructuració topològica i construcció dels nous elements, la traçabilitat dels elements originals dels quals prové cada element nou. La superposició vectorial, en el cas de dades representades segons el model vectorial topològic, és, doncs, essencialment un procés d'estructuració topològica amb la complexitat afegida d'haver de mantenir la traçabilitat de la procedència de cada element nou respecte dels elements dels conjunts de dades originals.
Operacions de superposició vectorial
La superposició, en el cas vectorial, presenta diverses variants segons el tipus geomètric de cadascuna de les classes d'elements que cal intersecar, segons l'extensió geogràfica del conjunt de dades resultant i segons les operacions addicionals o el propòsit de la intersecció (relació, actualització, buidat, retallada, etc.).
Superposició segons la geometria dels elements
Idealment, tenint en compte els tres tipus bàsics d'elements geomètrics -punt, línia i polígon- hi hauria d'haver nou variants diferents de superposició segons la geometria dels elements a superposar. Tanmateix, pel fet de ser una intersecció, només hi ha sis variants de superposició, ja que la intersecció d'elements geomètrics de diferent dimensió (per exemple, punts i polígons) sempre dóna lloc a elements de la dimensió més petita d'entre les classes d'elements participants a la superposició, de manera que sis de les superposicions possibles són en realitat només tres variants diferents (per exemple, és el mateix superposar punts amb polígons que polígons amb punts). Així, les variants de superposició segons la geometria dels elements són les següents:
- Superposició de punts: És la superposició entre un conjunt de punts i un altre conjunt de punts diferent, que permet determinar quins punts d'un conjunt de dades tenen la mateixa posició que els punts de l'altre conjunt de dades i heretar-ne els atributs. És un tipus de superposició poc freqüent ja que, no havent de generar nous elements geomètrics, és més pràctic de resoldre mitjançant una unió espacial. D'altra banda, és poc probable que conjunts de punts independents tinguin posicions exactament coincidents, i per tant una intersecció estricta no sol donar cap resultat, mentre que una unió espacial emprant com a condició l'element més proper pot donar resultats satisfactoris.
- Superposició de punts i línies: És la superposició entre un conjunt de punts i un conjunt de línies, que permet determinar quins punts d'un conjunt de dades estan continguts dins les línies de l'altre conjunt de dades i heretar-ne els atributs. Com en el cas de la superposició de punts, la superposició de punts i línies no genera nous elements geomètrics i per tant és més eficient resoldre-la mitjançant una unió espacial. També en aquest cas, una unió espacial per proximitat sol donar millors resultats.
- Superposició de punts i polígons: És la superposició entre un conjunt de punts i un conjunt de polígons que permet determinar en quin polígon es troba cada punt i transferir-hi els atributs del polígon. Igualment és un cas que es resol preferiblement per mitjà d'una unió espacial, a menys que interessi generar un conjunt de dades nou, a part, amb el resultat.
- Superposició de línies: És la superposició entre línies de dos conjunts de dades diferents que permet determinar quines línies o parts de línies d'un conjunt de dades estan contingudes totalment o parcialment dins les línies de l'altre conjunt de dades i heretar-ne els atributs. En aquest cas és necessari efectuar la intersecció, que fragmenta les línies d'un conjunt de dades segons les línies de l'altre conjunt de dades, la qual cosa dóna lloc a un nou conjunt de línies.
- Superposició de línies i polígons: És la superposicióentre línies i polígons de conjunts de dades diferents que permet determinar quines línies o parts de línies estan contingudes dins de cada polígon i heretar-ne els atributs. El resultat d'una superposició de línia en polígon és un nou conjunt de línies, que resulten de divididir les línies originals a la intersecció amb les vores dels polígons, i que tenen els atributs inicials de cada línia més els del polígon corresponent.
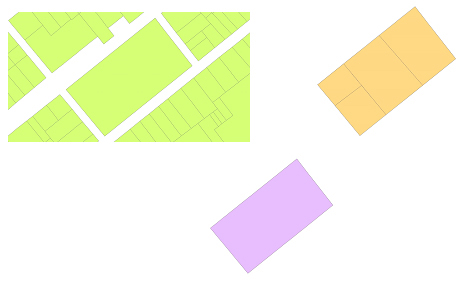
- Superposició de línies i polígons: És la superposició entre dos conjunts de polígons per a produir un nou conjunt de polígons que duu associats els atributs dels dos conjunts de polígons intersecats. És, de molt, el cas més freqüent de superposició.
Superposició segons l'extensió geogràfica
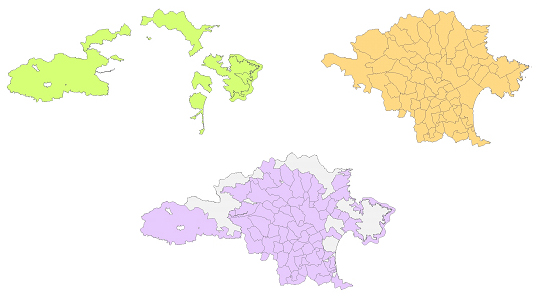
En el cas que els conjunts de dades a superposar tinguin extensions geogràfiques diferents, hi ha un seguit de variants de superposició que permeten decidir quina extensió tindrà el conjunt de dades resultant. En tots els casos, però, l'operació de superposició fa exactament el mateix, interseca els elements dels dos conjunts de dades i assigna als nous elements els atributs procedents dels elements dels dos conjunts de dades superposats. El que varia és només l'extensió geogràfica del conjunt de dades resultant i, en conseqüència, la disponibilitat de la informació de les parts de cad conjunt de dades que no s'encavalquen entre si o, dit d'una altra manera, la disponibilitat de les parts del territori per a les quals només és disposa d'una de les dues informacions superposades.
La lògica de les opcions de superposició segons l'extensió geogràfica segueix la lògica de conjunts i els noms de les variants coincideixen amb els dels corresponents operadors lògics. Les variants de superposició possibles segons l'extensió geogràfica són les següents. La majoria són aplicables a la superposició entre elements geomètrics de qualsevol tipus.
- Identitat: És la modalitat de superposició el resultat de la qual cobreix només l'extensió geogràfica d'un dels dos conjunts de dades originals objecte de la superposició.
- Intersecció: És la modalitat de superposició el resultat de la qual cobreix només l'extensió geogràfica comuna als dos conjunts de dades originals.
- Unió: És la modalitat de superposició el resultat de la qual cobreix només l'extensió geogràfica conjunta des dos conjunts de dades originals. La unió s'aplica només a la superposició de polígons.
- Diferència simètrica: És la modalitat de superposició el resultat de la qual cobreix només l'extensió geogràfica en què no hi ha encavalcament entre els dos conjunts de dades o, dit d'altra manera, l'extensió en què només hi ha informació d'un dels dos conjunts de dades. El resultat de la diferència simètrica és el complementari del resultat de la intersecció.
Superposició segons el propòsit de la intersecció
El principal propòsit de la superposició és relacionar els elements de dos conjunts de dades que representen entitats o fenòmens geogràfics diferents, generalment amb finalitats d'anàlisi, per bé que també s'utilitza amb finalitats de manipulació de dades com a operació auxiliar per a produir, refinar o derivar dades geoespacials. A més, a part de l'operació general de superposició, que realitza la intersecció dels elements, hi ha un seguit d'operacions especialitzades que utilitzen la intersecció per a propòsits clarament destinats a manipulació de dades com és ara retallar una part de la informació segons un àmbit territorial, actualitzar parcialment un conjunt de dades amb la informació de l'altre, etc. Les principals operacions de superposició destinades a la manipulació de dades són les següents.
- Retallada: És una superposició que talla i extreu en un conjunt de dades a part els elements d'un conjunt de dades continguts totalment o parcialment dins del contorn general definit per la totalitat dels elements poligonals d'un altre conjunt de dades.
- Buidat: És una superposició que elimina o esborra els elements o parts d'elements d'un conjunt de dades a l'interior del contorn general definit per la totalitat dels elements poligonals d'un altre conjunt de dades.
- Actualització: És una superposició que incorpora un conjunt d'elements nous a una classe d'elements d'un conjunt de dades geoespacials substituint els elements existents amb què coincideixen totalment o parcialment els elements nous.
- Divisió: És una superposició que divideix un conjunt de dades en conjunts de dades separats corresponents als polígons d'un altre conjunt de dades que defineix la divisió en parts del conjunt de dades original.
Operacions de superposició ràster
La geometria fixa del model de dades ràster fa innecessària la intersecció geomètrica dels conjunts de dades ràster per tal de poder relacionar-los. Les cel·les dels diferents conjunts de dades ràster tenen la mateixa posició i ocupen la mateixa extensió, i per tant es corresponen i són directament comparables. Per a relacionar dos, o més, conjunts de dades ràster basta comparar, operar o combinar els valors de les cel·les homòlogues. Normalment, la majoria de programes de SIG ràster operen només amb ràsters de la mateixa resolució espacial. Alguns programes de SIG, però, ofereixen la possibilitat d'operar entre si ràsters de diferent resolució espacial i escollir, si convé, una altra resolució espacial diferent per al resultat, efectuant el(s) remostreig(s) necessaris sobre la marxa.
Les operacions de superposició ràster, doncs, són moltes i molt variades, ja que pràcticament qualsevol operació entre els valors de les cel·les de dos o més ràsters es pot considerar una superposició o, si més no, una combinació de ràsters. De fet, el concepte d'àlgebra de mapes ràster (Tomlin, 1980; 1990), en tant que sistema d'operacions que genera nous conjunts de dades geoespacials derivats per combinació o per transformació de conjunts de dades geoespacials existents, és una generalització del concepte de superposició de mapes ràster.
Això no obstant, la superposició ràster pròpiament dita, que equival conceptualment a la superposició vectorial de polígons, es limita a les operacions aritmètiques o combinatòries sobre els valors de les cel·les homòlogues de dos o més conjunts de dades ràster que produeixen el conjunt de posicions (cel·les) on es dóna cada una de les combinacions de valors de dos o més atributs. Tot i així, les possibilitats d'operacions diferents són encara força àmplies.
Bàsicament, hi ha dues aproximacions principals per a resoldre la superposició ràster: la superposició de ràsters binaris i l'encreuament de ràsters categòrics.
La superposició de ràsters binaris (amb valors 0 o 1) permet obtenir mitjançant un producte les cel·les on es dóna una determinada combinació de valors de dos (o més) atributs, o bé mitjançant una suma les cel·les on es dóna una o altra de les categories d'interès. La superposició de ràsters binaris requereix una reclassificació prèvia els ràsters originals per aïllar les cel·les amb els valors d'una categoria determinada de cada un dels ràsters. Aquesta aproximació és útil quan interessa només una determinada combinació de valors dels atributs dels dos (o més) ràsters, o un nombre reduït de combinacions, ja que obliga a fer molts passos i a generar força conjunts de dades ràster per a cada combinació d'interès.
Quan el que interessa, en canvi, són totes les combinacions de valors dels atributs representats en els dos (o més) ràsters, l'aproximació més eficient és l'encreuament de ràsters categòrics, que identifica amb un valor únic cada una de les combinacions de valors presents i l'assigna a la cel·la on es produeix la combinació. El resultat és un ràster nou amb valors que expressen les diferents combinacions dels dos (o més) ràsters superposats. L'encreuament de ràsters categòrics resol en un sol pas la determinació de totes les combinacions de valors de les cel·les dels ràsters originals, que és equivalent a la intersecció geomètrica de dos (o més) conjunts de polígons i la combinació dels seus respectius atributs.
La superposició ponderada és una superposició ràster que es fa servir en les anàlisis multicriteri, com per exemple els models d'idoneïtat o d'impacte, i que consisteix a calcular la suma ponderada dels valors de dos o més ràsters. Per tal d'efectuar la superposició ponderada, els valors de les cel·les dels ràsters que cal combinar aritmèticament es normalitzen prèviament segons una mateixa escala, es ponderen multiplicant-los pel pes relatiu atribuït a cadascun dels ràsters i finalment es sumen per obtenir el resultat de la superposició ponderada en forma d'índex, generalment de 0 a 100, que indica l'aptitud o el grau d'adequació de cada punt del territori en relació a l'objectiu de l'anàlisi. Aquest tipus d'anàlisi també es pot realitzar amb dades vectorials, fent primer la intersecció geomètrica de tots els conjunts de dades i calculant després la suma ponderada dels valors dels atríbuts dels polígons resultants de la intersecció geomètrica.
Temes relacionats
- Àlgebra de mapes
- Anàlisi multicriteri
- Estructuració topològica
- Model de dades ràster
- Model de dades vectorial
- Sistemes d’informació geogràfica
- Unió espacial
- Unió relacional
Referències
Cowen, D.J. (1988) "GIS versus CAD versus DBMS: What are the differences?", Photogrammetric Engineering and Remote Sensing, 54, 11, 1551-1555.
McHarg, I.L. (1969) Design with Nature, New York: Natural History Press.
Peucker, T.K. and Chrisman, N. (1975) "Cartographic data structures", American Cartographer, 2, 1, 55-69.
Sinton, D.F. and Steinitz, C.F. (1969) GRID: A user's manual, Cambridge, Massachussets: Laboratory for Computer Graphics and Spatial Analysis, Graduate School of Design, Harvard University.
Tomlin, C.D. (1980) The Map Analysis Package. Connecticut: Yale School of Forestry and Environmental Studies.
Tomlin, C.D. (1990) Geographic Information Systems and Cartographic Modeling, Engleshy;wood Cliffs, New Jersey: Prentice Hall.
Tomlinson, R.F. (1967) An Introduction to the Geographic Information System of the Canada Land Inventory. Ottawa: Department of Forestry and Rural Development.
Tomlinson, R.F. (1980) "The handling of data for natural resources development" in Proceedings of Workshop on Information Requirements for Dvelopment Planning in Developing Countries. Enschede: ITC.
Tomlinson, R.F.; Calkins, H.W. and Marble, D.F. (1976) Computer handling of geographical data. Geneva: UNESCO.
White, D. (1977) "A new method of polygon overlay" in Dutton, G. H. (ed.) Proceedings of the Advanced Study Symposium on Topological Data Structures for Geographic Information Systems. Cambridge, Massachussets: Laboratory for Computer Graphics and Spatial Analysis, Harvard University.
White, D. (1990) "The polygon overlay operation" in M.F. Goodchild and K.K. Kemp (eds.) NCGIA Core Curriculum in GIS, Unit 34. National Center for Geographic Information and Analysis, University of California, Santa Barbara.
Lectures recomanades
Burrough, P.A. (1986) Principles of Geographical Information Systems for Land Resources Assessment, Oxford, UK, Clarendon Press. Chapter 5.
Tomlinson, R.F. (1980) "The handling of data for natural resources development" in Proceedings of Workshop on Information Requirements for Dvelopment Planning in Developing Countries. Enschede: ITC.

 Contacte
Contacte