Autor: Dr. Joan Nunes. Universitat Autònoma de Barcelona
Promotor: Institut Cartogràfic de Catalunya, 2013
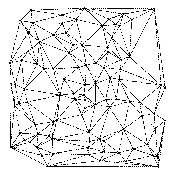
Una xarxa irregular de triangles (triangulated irregular network, TIN) és un model de dades específic per a representar superfícies en forma digital utilitzat en els sistemes d’informació geogràfica. Una xarxa irregular de triangles representa una superfície mitjançant facetes triangulars irregulars, formades a partir d'un conjunt de punts de mostreig, amb coordenades x, y i z, distribuïts de manera variable per a reflectir els canvis de forma significatius de la superfície. L'obtenció dels triangles a partir dels punts es basa generalment en la triangulació de Delaunay, encara que també s'utilitzen altres mètodes alternativament o de forma conjunta.
El model de dades TIN es pot aplicar a la representació de qualsevol superfície, però s'utilitza principalment per a representar la superfície del relleu en els models digitals d'elevacions, com a alternativa a la representació mitjançant el model de dades ràster. El model de dades TIN té alguns avantatges respecte a la representació ràster a l'hora de representar superfícies, entre els quals destaquen la major adaptabilitat a les formes del terreny o de la superfície representada, la possibilitat d'incorporar explícitament elements que defineixen la forma del terreny (cursos d'aigua, carenes, pics, etc.), la no-dependència d'un interval de mostreig regular que quan és massa ample pot fer perdre detalls importants de la variació de forma de la superfície, i el fet d'evitar l'excés de dades redundants en les zones en què la variació de la superfície és escassa. El model de dades ràster, per la seva part, té els avantatges incontestables d'una major simplicitat de representació i de càlcul, major disponibilitat de dades i de programes per a tractar-les, i major adequació als mètodes d'interpolació i d'anàlisi de la variació espacial, com és ara l'estadística espacial i la geoestadística.
Sumari:
Origen
L'ús d'una xarxa irregular de triangles com a model de dades per a representar superfícies, en particular el relleu del terreny, és una aportació genuïna de l'àmbit dels sistemes d’informació geogràfica, per bé que el concepte de xarxa irregular de triangles i, en concret, la triangulació de Delaunay, ideada pel matemàtic rus Boris Nikolaevich Delaunay, són força anteriors (Delaunay, 1934).
El model de dades TIN, en l'àmbit dels sistemes d’informació geogràfica, va ser formulat a la dècada de 1970, entre d'altres, per Thomas Peucker (Peucker, 1972; Peucker and Chrisman, 1975; Peucker et al., 1975; Peucker et al., 1978), encara que probablement hi ha diversos origens paral·lels (Dueppe and Gottschalk, 1970; Rhynsburger, 1973; Gates, 1974; Bauhuber et al., 1975; Gold et al., 1977).
Durant la dècada e 1970 es desenvoluparen diversos prototips de programes de càlcul de xarxes irregulars de triangles (Fowler, 1977), el primer dels quals, creat l'any 1973, s'atribueix a Randolph W. Franklin (2006) de Simon Fraser University. A la dècada de 1980 aparegueren els primers programes comercials que utilitzaven el model de dades TIN, alguns com a programes independents de modelització del terreny i càlcul d'isolínies, d'altres incorporats en programes de SIG.
Definició
Sovint es considera el model de dades TIN com un tipus de model de dades vectorial. No obstant, si bé és cert que els triangles d'una xarxa irregular de triangles formen una tessel·lació o mosaic d'àrees disjuntes, donades les característiques particulars de la xarxa triangular (totes les àrees són triangles, tots els vèrtexs són nodes, cada aresta es defineix només per dos nodes, cada triangle té només tres arestes, tres nodes i tres triangles veïns,...), aquesta no es representa mitjançant l'estructura topològica habitual del model vectorial topològic ni per mitjà de la llista de coordenades del model vectorial sense topologia, sinó que es representa directament per mitjà dels nodes o dels triangles. Altrament, la representació per mitjà de xarxes irregulars de triangles del model de dades TIN està pensada per a representar de manera aproximada formes tridimensionals contínues en tres dimensions, és a dir, superfícies, en lloc de formes bidimensionals discretes (polígons) en el pla. Aquestes especificitats fan de la xarxa irregular de triangles, aplicada a la representació de superfícies, un model de dades en si mateix, amb estructures, regles i operacions pròpies.
Els components del model de dades TIN són els següents:
Elements de TIN:
- nodes: són els vèrtexs dels triangles, corresponen als punts del mostreig espacial original o a una selecció dels punts significatius, posseeixen coordenades x, y i z, i són el component fonamental de la triangulació (els canvis en els punts modifiquen la representació de la superfície) i del model de dades (la major part del model de dades es defineix i emmagatzema per mitjà dels nodes).
- arestes: són els segments lineals entre cada parell de nodes, que formen cada un dels costats dels triangles.
- triangles: són cadascuna de les facetes que formen una superfície representada com a xarxa irregular de triangles. Cada faceta o triangle determina un pla, amb un pendent i una orientació que s'emmagatzemen com a atributs de la faceta.
- polígon convex mínim: és el contorn definit pel conjunt de triangles que formen una xarxa irregular de triangles. En cas que la xarxa irregular de triangles sigui discontínua i cobreixi diverses àrees separades, tindrà tants polígons convexos mínims com àrees separades. A menys que l'usuari imposi un contorn arbitrari que retalli l'àrea coberta pel TIN, el contorn d'una xarxa irregular de triangles és sempre un polígon convex.
Relacions topològiques en un TIN:
El model de dades TIN és un model de dades topològic, atès que la informació de relacions entre nodes, arestes i triangles hi és explícita.
- Cada node té un nombre variable de nodes veïns. La llista dels nodes veïns de cada node defineix les arestes en què participa el node i, implícitament, els triangles.
- Cada aresta té informació topològica sobre els nodes que connecta i els triangles que delimita.
- Cada triangle té informació topològica sobre els tres nodes que el formen, les tres arestes que el delimiten i els tres triangles adjacents.
La informació topològica de nodes, arestes i triangles d'una xarxa irregular de triangles és redundant, i per tant és suficient emmagatzemar només les relacions d'un dels tres tipus d'elements del TIN. El més habitual és emmagatzemar les dels nodes o les dels triangles.
Mètodes de triangulació
L'elecció correcta dels punts a partir dels quals es genera la xarxa irregular de triangles és fonamental per a la millor o pitjor adequació del TIN a la superfície a representar. Per aquest motiu no sempre s'utilitzen tots els punts del mostreig espacial original ni els punts originals són necessàriament suficients i cal afegir-ne d'altres de més significatius o simplement augmentar el nombre de punts a les zones de major variació de la superfície mitjançant una densificació de TIN. En el cas d'utilitzar una xarxa irregular de triangles per a representar un model digital d'elevacions, la densitat de punts i l'elecció d'aquests ve guiada per les formes del relleu i hi ha diversos algorismes de selecció de punts. En el cas dels models digitals d'elevacions també és possible incorporar a la triangulació elements d'informació addicionals per tal d'adaptar la forma de la superfície del relleu a aquestes formes o línies estructurals.
Independentment de la selecció dels punts i dels procediments existents per a fer la selecció, el procés de creació dels triangles a partir d'un conjunt de punts donat és la triangulació. Hi ha més d'un mètode de triangulació, però el més emprat en els sistemes d’informació geogràfica és la triangulació de Delaunay. El supòsit bàsic de qualsevol mètode a l'hora de crear els triangles és dividir l'espai segons la proximitat dels nodes, ja que la representació de la superfície és lògicament més acurada en els nodes dels triangles, atès que tenen valors mesurats, que en la resta del triangle on els valors de superfície són interpolats.
En aquest sentit, és desitjable que els triangles siguin "amples", amb angles propers a 60 graus, ja que això assegura que tot punt de la superfície és el més a prop possible d'un node. Una bona xarxa irregular de triangles conté, per tant, el major nombre possible de triangles amples i tan pocs triangles estrets com sigui possible.
Un altre dels errors a evitar en la creació d'una xarxa irregular de triangles és la formació de triangles plans; és a dir, triangles d'igual coordenada o valor z en tots els seus nodes. Normalment, l'aparició de triangles plans és indicativa d'un mostreig espacial inadequat, bé per excés de punts en zones d'escassa variació de la superfície, bé per elecció de punts amb un cert biaix, com en el cas de punts al llarg de corbes de nivell, que tenen el mateix valor de superfície.
Un dels primers mètodes de triangulació emprats (Dueppe and Gottschalk, 1970) és el d'ordenació per distància. Aquest mètode consisteix a calcular la distància entre tots els parells de punts, ordenar els parells en ordre creixent de distància, connectar el parell de punts més propers creant l'aresta corresponent, i continuar connectant el següent parell de punts més propers si l'aresta resultant no creua cap aresta creada prèviament fins a exhaurir la llista de parells de punts. En acabar la llista, tots els punts estan connectats formant triangles. El principal inconvenient d'aquest mètode és la tendència que té a produir força polígons estrets en lloc dels triangles amples desitjats (Poiker, 1990).
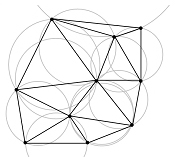
La triangulació de Dealunay és una xarxa irregular de triangles generada a partir d'un conjunt de punts que compleix la regla, anomenada criteri de Delaunay, que el cercle en què s'inscriu cada triangle no conté altres punts del mostreig original que els tres vèrtexs que defineixen el triangle.
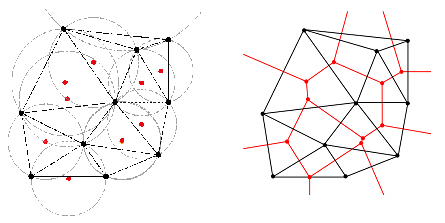
El compliment del criteri de Delaunay assegura que tot punt de la superfície generada mitjançant el conjunt dels triangles és tan proper com sigui possible a un node d'un triangle, de manera que s'obtenen polígons generalment amples, excepte a les vores i entre punts molt propers. Pel fet de minimitzar la distància de qualsevol punt als nodes dels triangles, les bisectrius dels costats dels triangles donen lloc directament a una partició en polígons de Thiessen o diagrama de Voronoi, i viceversa, unint els centres de polígons de Thiessen veïns, s'obté la triangulació de Delaunay, ja que ambdues particions són mútuament el graf dual l'una de l'altra.
La triangulació obtinguda mitjançant el criteri de Delaunay té les propietats de ser única per a cada conjunt de punts donat, de ser independent de l'ordre de processament dels punts i de generar sempre un contorn global de la xarxa irregular de triangles que és el polígon convex mínim que inclou tots els punts.
Per les seves propietats, la triangulació de Delaunay és el mètode més utilitzat en els sistemes d’informació geogràfica s'utilitza per a generar xarxes irregulars de triangles i particions de polígons de Thiessen. Les primeres aplicacions d'aquest mètode a la construcció de xarxes irregulars de triangles daten de principis de la dècada de 1970 (Rhynsburger, 1973).
Hi ha diferents procediments per a generar la triangulació de Delaunay d'un conjunt de punts (Poiker, 1990). Els més utilitzats són dos procediments alternatius. Un procediment parteix de generar el polígon convex mínim i progressa cap a l'interior de la mostra de punts. L'altre parteix del parell de punts més propers, cerca un tercer punt tal que el cercle definit pels tres punts no contingui cap altre punt, i progressa cap a l'exterior repetint el procés amb els punts més propers als nodes de les arestes que es van formant.
Incorporació de línies estructurals
Un dels avantatges importants d'usar una xarxa irregular de triangles com a model de dades per a representar superfícies és la capacitat que té el model de dades TIN de reflectir els canvis sobtats de pendent en la superfície alineant les arestes dels triangles amb les línies estructurals que defineixen aquests canvis de pendent i per tant de forma de la superfície. Aquest és un aspecte important en el cas d'emprar el model de dades TIN per a representar models digitals d'elevacions, ja que en el cas del relleu és possible disposar de línies estructurals com carenes i fons de vall que convé incloure en la xarxa irregular de triangles per tal de representar adequadament les formes genuïnes del relleu.
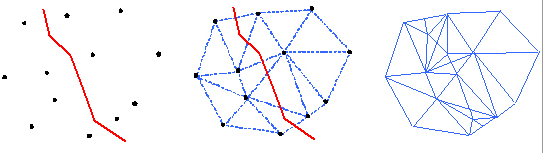
La incorporació de línies estructurals en el procés de construcció de la xarxa irregular de triangles és un mètode emprat en alguns programes de SIG per tal de produir resultats més acurats a l'hora de generar models digitals d'elevacions mitjançant el model de dades TIN. El mètode consisteix a incorporar les línies estructurals després d'haver generat una primera xarxa de triangles mitjançant el criteri de Delaunay i adaptar la xarxa triangles de manera que les arestes dels triangles coincideixen amb les línies estructurals. El resultat generalment, ja no manté el criteri de Delaunay, però té el valor afegit d'incloure un cert conjunt de formes genuïnes del relleu.
Hi ha dos tipus diferents de línies estructurals, les línies de continuïtat i les línies de ruptura, que tenen diferent efecte posteriorment en la interpolació de valors a través de la superfície representada per la xarxa irregular de triangles, però no en la creació de la triangulació en sí. Tots dos tipus de línies estructurals es recullen per igual fent coincidir els costats dels triangles amb l'element lineal per tal que aquest es mantingui com a tal en la superfície resultant.
Les línies de continuïtat (soft structure line, softline) són línies estructurals en una xarxa irregular de triangles que no representa una discontinuïtat en el pendent de la superfície. Una línia de continuïtat s'introdueix en la triangulació tan sols a efectes de fer-la explícita per mitjà de les arestes dels triangles, per a recollir-ne la forma o per a mantenir els valors coneguts de la superfície al llarg de la línia. Les carreteres o les conduccions són exemples de línies de continuïtat. Les línies de continuïtat no actuen com a barrera en el procés d'interpolació a través de la superfície representada per la xarxa irregular de triangles.
Les línies de ruptura (breakline, hard structure line, hardline) són línies estructurals que suposen una discontinuïtat genuïna en el pendent de la superfície. Pel fet d'interrompre la continuïtat del pendent, els costats dels triangles d'una xarxa irregular de triangles han de coincidir necessàriament amb la línia de ruptura. Les línies de ruptura actuen, a més, com a barreres en el procés d'interpolació, de manera que els triangles adjacents no es tenen en compte per a crear una superfície suavitzada i es produeix, així, la discontinuïtat. El valor de la superfície al llarg de la línia de ruptura pot ser constant (per exemple, les vores d'un llac) o variable (per exemple, un riu o una carena).
Emmagatzematge
Una xarxa irregular de triangles s'emmagatzema necessàriament com un conjunt de dades a part per si mateixa, formant el que es coneix com un conjunt de dades TIN. Hi ha diferents estructures de dades per emmagatzemar un TIN. Les més habituals són l'emmagatzematge dels punts i l'emmagatzematge dels triangles.
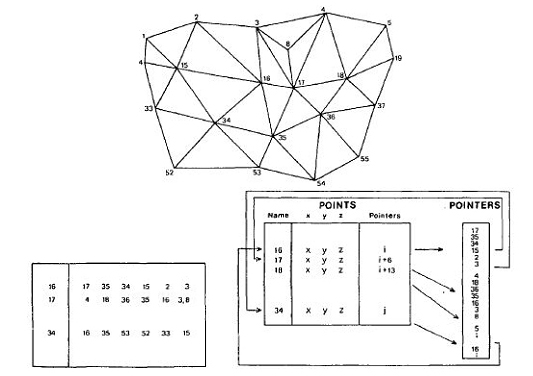
L'emmagatzematge dels punts d'un TIN emmagatzema per a cada node la identificació, les coordenades x, y i z, la referència de cada un dels nodes veïns del node en sentit horari o antihorari, segons els programes. L'emmagatzematge per mitjà dels punts és l'estructura de dades original del model de dades TIN (Peucker et al, 1975; 1978).
L'emmagatzematge dels triangles d'un TIN emmagatzema per a cada triangle la identificació del triangle, la identificació i les coordenades x, y i z dels tres nodes, la referència als tres triangles veïns. Les coordenades dels nodes se solen guardar en un fitxer a part al qual es fa referència des del fitxer de triangles, a fi d'evitar l'emmagatzematge repetit de les coordenades dels nodes ja que cada node és compartit per un cert nombre de triangles. Addicionalment, en el cas d'incorporar línies estructurals a la xarxa irregular de triangles, per a cada aresta s'emmagatzema si és una línia estructural i de quin tipus.
Les dues estructures de dades es poden derivar l'una de l'altra i cada una es necessita per a diferents tipus d'operacions derivades a partir del TIN (per exemple, la interpolació i el càlcul d'isolínies són més fàcils i ràpides a partir dels punts, mentre que el càlcul de pendents i orientacions es fa a partir dels triangles). L'emmagatzematge dels punts és lleugerament més compacte, mentre que l'emmagatzematge dels polígons és més explícit i conté gairebé tota la informació de triangles i punts. Generalment, l'emmagatzematge dels triangles ha estat l'estructura de dades finalment adoptada per la majoria de programes.
Temes relacionats
- Estadística espacial
- Geoestadística
- Interpolació
- Model de dades ràster
- Model de dades vectorial
- Model digital d'elevacions
- Mostreig espacial
- Polígons de Thiessen
- Sistemes d’informació geogràfica
- Superfície
Referències
Bauhuber, F.; Erlacher, V. and Gunther, P. (1975) "A Programming System for the Manipulation of Digital Terrain Models" (in German). Organ der Deutschen Gesellschaft fur Photogrammetrie, 43, 104-107.
Delaunay, B. (1934) "Sur la sphère vide", Izvestia Akademii Nauk SSSR, Otdelenie Matematicheskikh i Estestvennykh Nauk, 7, 793–800.
Dueppe, R. D. and Gottschalk, H. J. (1970) "Automatische Interpolation von Isolinien bei willkuerlich verteilten Stuetzpunkten", Allgemeine Vermessungs-Nachrichten, 129, 10, 423-426.
Fowler, R.J. (1977) DELTRI: An Efficient Program for Producing Delaunay Triangulations. Tech. Rept. 18, ONR Contract #NOOO14-75-C-0886. Burnaby, British Columbia, Canada: Department of Geography, Simon Fraser University.
Franklin, R.W. (2006) "Triangulated Irregular Network".
Gates, W.E. (1974) A Land Based Modelling System for Water Quality Management Studies, Report for Virginia Electric and Power.
Gold, C.M.; Charters, T.D. and Ramsden, J. (1977) "Automated Contour Mapping Using Triangular Element Data Structures and an Interpolant Over Each Irregular Triangular Domain" in Proceedings of SIGGRAPH'77, San Jose, California.
Peucker, T.K. (1972) Computer Cartography. Commission on College Geography, Resource Paper No. 17, Washington DC: Association of American Geographers.
Peucker, T.K. and Chrisman, N. (1975) "Cartographic data structures", American Cartographer, 2(1), 55-69.
Peucker, T.K.; Fowler, R.J.; Little, J.J. and Mark, D.M. (1975) Digital Representation of Three-Dimensional Surfaces by Triangulated Irregular Networks (TIN). Tech. Rept. 10, ONR Contract #N00014-75-C-0886. Burnaby, British Columbia, Canada: Department of Geography, Simon Fraser University.
Peucker, T.K.; Fowler, R.J.; Little, J.J. and Mark, D.M. (1978) "The Triangulated Irregular Network" in Proceedings ofDigital Terrain Models (DTM) Symposium, St. Louis, Missouri. American Society of Photogrammetry.
Poiker, T.K. [abans Peucker] (1990) "The TIN Model" in M.F. Goodchild and K.K. Kemp (eds.) NCGIA Core Curriculum in GIS, Unit 39. National Center for Geographic Information and Analysis, University of California, Santa Barbara.
Rhynsburger, D. (1973) "Analytic Delineation of Thiessen Polygons", Geographical Analysis, 5, 2, 133-144.
Lectures recomanades
Burrough, P.A. (1986) Principles of Geographical Information Systems for Land Resources Assessment, Oxford, UK, Clarendon Press. Chapter 3.
Peucker, T.K.; Fowler, R.J.; Little, J.J. and Mark, D.M. (1978) "The Triangulated Irregular Network" in Proceedings ofDigital Terrain Models (DTM) Symposium, St. Louis, Missouri. American Society of Photogrammetry.

 Contacte
Contacte