Autor: Dr. Joan Nunes. Universitat Autònoma de Barcelona
Promotor: Institut Cartogràfic de Catalunya, 2013
En els sistemes d’informació geogràfica (SIG), una àrea d'influència (buffer) és una àrea definida per una distància fixa a l'entorn d'un element espacial (punt, línia o polígon), que s'utilitza per a fer anàlisis de distància. El cas específic d'àrea d'influència entorn d'un element lineal s'anomena de vegades corredor i l'anàlisi corresponent anàlisi de corredors. Àrea d'influència no s'ha de confondre amb àrea de proximitat, que és l'àrea definida a l'entorn de cada punt d'un conjunt de punts donat, que delimita l'espai més pròxim a cada punt i que s'obté mitjançant una partició de polígons de Thiessen.
El càlcul d'àrees d'influència és una operació espacial bàsica de geoprocessament de dades vectorials, que, juntament amb la selecció per distància, l'anàlisi de l'element més proper, el càlcul de matrius de distància entre elements i l'anàlisi de proximitat, forma el grup d'operacions de SIG d'anàlisi de distància.
El càlcul d'àrees d'influència es pot realitzar també amb dades de tipus ràster, per mitjà d'operacions de geoprocessament ràster, com la dilatació o l'anàlisi de distància euclidiana, que proporcionen resultats equivalents als obtinguts amb dades vectorials.
L'anàlisi d'àrees d'influència serveix per a determinar què hi ha a l'entorn de cada element, mitjançant la combinació posterior amb altres conjunts de dades, o bé per a definir àrees de protecció, d'impacte, etc, que poden ser incorporades com a condicions en altres anàlisis posteriors. L'anàlisi d'àrees d'influència s'utilitza en tots els camps d'aplicació dels sistemes d’informació geogràfica, entre els quals i especialment, les aplicacions d'avaluació d'impacte ambiental, de gestió de recursos naturals, de planificació, localització i anàlisi de la cobertura de serveis, de gestió forestal o d'anàlisi d'àrees de mercat en geomàrqueting.
Sumari:
- Origen
- Definició
- Variants d'àrees d'influència
3.1 Àrees d'influència individuals o agregades
3.2 Àrees d'influència de distància variable
3.3 Àrees d'influència parcials
3.4 Àrees d'influència de múltiples corones
3.5 Àrees d'influència euclidianes o geodèsiques - Ànàlisi d'àrees d'influència amb dades ràster
4.1 Dilatació
4.2 Anàlisi de distància euclidiana - Temes relacionats
- Referències
- Lectures recomanades
Origen
El càlcul d'àrees d'influència és una operació bàsica dels sistemes d’informació geogràfica, contemplada en el programari de SIG vectorial des del principi (Tomlinson, 1967, 1980; Tomlinson et al., 1976). Igualment, les operacions ràster equivalents són també de les primeres operacions implementades en el programari de SIG ràster (Sinton and Steinitz, 1969; Tomlin, 1980).
Com la majoria d'operacions bàsiques d'anàlisi cartogràfica, el càlcul d'àrees d'influència té el seu antecedent en operacions manuals de manipulació d'informació cartogràfica realitzades en aplicacions de planificació, d'urbanisme, d'arquitectura del paisatge i de gestió forestal o de recursos naturals (McHarg, 1969). Tanmateix, és probable que fins a la informatització de la cartografia i el desenvolupament dels sistemes d’informació geogràfica, hagi estat una operació efectuada de forma limitada per la laboriositat del càlcul i dibuix manual.
Definició
El càlcul d'àrees d'influència és un procés intensiu de càlcul que comprèn diverses etapes. La primera etapa és el càlcul de l'àrea d'influència individual de cada element. El procés per calcular l'àrea d'influència individual d'un element recorre la seqüència de vèrtexs de l'element i genera per a cada vèrtex punts desplaçats a banda i banda, a la distància especificada de l'àrea d'influència. Després, es forma el polígon de l'àrea d'influència connectant els punts desplaçats mitjançant segments rectes i arcs de cercle. El procés és equivalent a traçar un cercle de radi igual a la distància de l'àrea d'influència en cada un dels vèrtexs de l'element i traçar línies paral·leles a banda i banda de cada segment original entre parells de vèrtexs de manera que siguin tangents als cercles entorn de cada vèrtex. La figura delimitada pels segments de recta paral·lels i els arcs de cercle que resten d'intersecar-se mútuament és l'àrea d'influència de distància desitjada.
Lògicament en el cas de calcular l'àrea d'influència d'un punt el procés consisteix simplement a traçar el cercle de radi corresponent a la distància de l'àrea d'influència.
Un cop es disposa de les àrees d'influència individuals de cada element, l'operació de càlcul d'àrees d'influència pot acabar si el procediment implementat en el programa de SIG o l'opció escollida per l'usuari és mantenir les àrees d'influència individuals separades. Si no, l'operació continua amb dues etapes addicionals per tal d'obtenir àrees d'influència agregades. Una segona etapa que efectua la superposició de les àrees d'influència individuals a fi d'integrar-les en un mateix pla mitjançant la intersecció de totes. I, finalment, una tercera etapa duu a terme l'agregació espacial dels polígons resultants de la intersecció d'àrees d'influència individuals per obtenir l'àrea d'influència agregada, emprant com a criteri d'agregació l'atribut dels polígons que indica que són dins l'àrea d'influència i eventualment, segons els programes, altres atributs addicionals. El resultat és una àrea d'influència agregada, global, per a cada conjunt d'àrees d'influència individuals contigües o encavalcades entre si.
Variants d'àrees d'influència
Hi ha nombroses variants d'àrees d'influència segons el nombre major o menor d'opcions que ofereixen els diferents programes de SIG en relació a criteris com generar àrees d'influència individuals o agregades, utilitzar distàncies iguals o variables per a cada element, generar àrees d'influència parcials només en un costat dels elements o generar simultàniament múltiples àrees d'influència
Àrees d'influència individuals o agregades
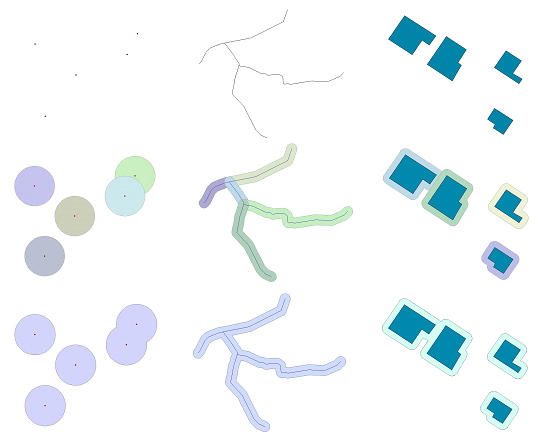
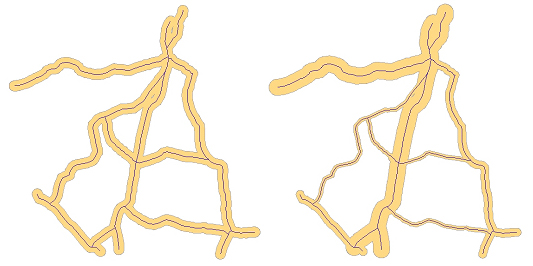
El càlcul d'àrees d'influència individuals produeix un polígon d'àrea d'influència per a cada element original, que inevitablement s'encavalca amb els polígons d'àrea d'influència d'altres elements propers, però que conté un atribut que identifica a quin element pertany. En canvi, el càlcul d'àrees d'influència agregades interseca i uneix tots els polígons d'àrea d'influència individuals contigus o encavalcats i produeix polígons d'àrea d'influència globals.
Les àrees d'influència individuals tenen interès quan es vol saber a quin element correspon cada àrea d'influència (per exemple, a quina carretera). Les àrees d'influència agregades només donen informació genèrica de l'espai a una certa distància d'un tipus d'element (per exemple, 100 m de distància a qualsevol carretera).
Les àrees d'influència individuals són possibles en aquells programes de SIG que utilitzen un model de dades vectorial sense topologia; és a dir, un model vectorial de polígons explícits o d'elements simples, en el qual els polígons són independents els uns dels altres i poden existir per tant polígons encavalcats o apilats. En aquests programes, el càlcul d'àrees d'influència individuals o agregades és una opció que l'usuari pot decidir. En tant que opció, alguns programes afegeixen fins i tot l'opció d'agregar només selectivament part de les àrees d'influència individual utilitzant atributs temàtics com a criteri d'agregació espacial, en lloc de simplement agregar totes les àrees d'influència individuals encavalcades, que també és una opció possible. En el model de dades vectorial sense topologia, convé tenir present també que l'agregació espacial de les àrees d'influència individuals en àrees d'influència agregades, tant si és completa com si és selectiva, pot produir elements multipart, cosa que pot no ser el resultat desitjat i que caldrà convertir a elements unipart.
Contràriament, les àrees d'influència agregades són obligatòries en els programes de SIG que utilitzen un model de dades vectorial topològic; és a dir, un model vectorial amb topologia planar, en el qual tots els elements han d'estar necessàriament en un mateix pla i per tant els polígons existents són sempre i necessàriament intersecció de tots els polígons presents en una determinada regió de l'espai. En aquest cas, donat que els polígons d'àrea d'influència individual no existeixen per si mateixos, sino com a fragments resultants d'intersecar-se amb altres, té més sentit l'agregació espacial de tots els fragments continus per a formar àrees d'influència genèriques. En els programes de SIG amb un model de dades vectorial topològic, les àrees d'influència agregades són l'única possibilitat i no ofereixen cap altra opció en aquest sentit a l'usuari. Les àrees d'influència agregades no posseeixen atributs que informin de la pertinença de cada àrea a un element determinat, ja que l'agregació elimina la possibilitat d'aquesta informació, però sí que tenen un atribut per indicar quins polígons són dins, és a dir àrea d'influència, i quins són fora. La necessitat d'aquest atribut és obligada en el model de dades vectorial topològic, ja que en la topologia planar els polígons inclosos dins d'altres polígons no són veritables forats, sinó un polígon més que, en el cas de les àrees d'influència, cal poder discriminar. En canvi, en el model de dades vectorial sense topologia, com que no es necessita informació de veïnatge entre polígons, poden existir veritables forats (àrees buides que no constitueixen un polígon) i per tant no és necessari l'atribut que diferencia entre dins i fora de l'àrea d'influència.
Històricament, donat que el model de dades vectorial topològic ha estat el predominant o considerat superior fins a mitjans de la dècada de 1990, les àrees d'influència agregades són anteriors a l'opció de mantenir separades les àrees d'influència individuals. El fet d'oferir com a opció un tipus o altre d'àrees d'influència és un reflex del canvi en el model de dades vectorial predominant en favor d'estructures de dades més simples que es produí a la segona meitat de la dècada de 1990, però també d'un canvi de sensibilitat vers un contingut d'informació geoespacial més ric i particularitzat, amb una major presència d'elements amb identitat pròpia, capaç de satisfer necessitats d'informació més diverses.
Àrees d'influència de distància variable
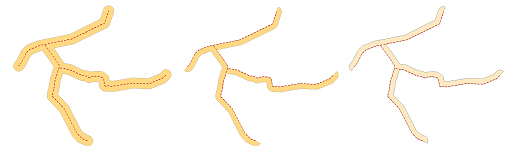
La possibilitat de definir les àrees d'influència mitjançant una distància variable, particular per a cada element, en funció del valor d'un atribut (per exemple, diferent distància segons el tipus de carretera), és una opció bàsica, oferta gairebé en tots els programes de SIG. Per poder aplicar aquesta opció, generalment, és necessari afegir un atribut a la taula d'atributs que indiqui la distància a aplicar a cada element, enlloc d'una distància fixa indicada globalment en efectuar l'operació. Segons que es tracti d'un o altre cas, s'obtindran àrees d'influència de distància variable o bé àrees d'influència de distància fixa.
El concepte bàsic d'àrea d'influència és la d'una àrea definida per una distància determinada al voltant d'un o més elements espacials. Això vol dir que l'àrea d'influència es genera per tots els costats de l'element espacial. Amb el temps, però, els programes de SIG han desenvolupat opcions d'àrea d'influència parcial, només a un costat de l'element espacial, que poden ser útils per a determinades aplicacions. La definició d'aquestes àrees d'influència parcials depèn del tipus d'element geomètric de què es tracti.
Àrees d'influència només a un costat de les línies
En el cas de les línies, les àrees d'influència parcials són àrees d'influència només a un costat, esquerre o dret, de la línia. La informació del costat d'una línia és coneguda sempre, ja que la seqüència de vèrtexs que constitueix la línia defineix un ordre que estableix el sentit de la línia. Prenent el sentit de la línia com a sentit de desplaçament, la caracterització dels costats de la línia com a esquerre o dret es correspon amb la definició natural d'aquests termes. En el cas de línies enregistrades segons el model de dades vectorial topològic aquesta informació queda emmagatzemada permanentment com a resultat del procés d'estructuració topològica. En el cas de línies en el model de dades vectorial sense topologia aquesta informació s'ha de deduir de la seqüència de vèrtexs cada cop que es necessita.
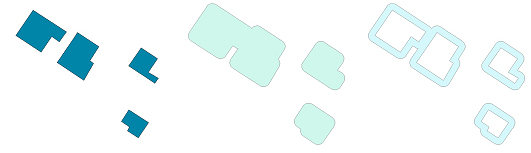
Àrees d'influència només a l'exterior dels polígons
En el cas dels polígons, les àrees d'influència parcials es defineixen també a un costat o altre del contorn del polígon, si bé en aquest cas es caracteritzen millor com exterior i interior, que no pas com esquerre o dret. D'altra banda, com que el costat interior és dins del polígon i no té interès com a àrea de distància, l'única àrea d'influència parcial contemplada en el cas dels polígons és l'àrea d'influència només a l'exterior dels polígons. El resultat és la part que queda de l'àrea d'influència completa un cop descomptat el polígon.
Opcions de forma dels extrems de l'àrea d'influència
En el cas de les àrees d'influència a l'entorn de línies, sol haver-hi l'opció de decidir la forma dels extrems de les àrees d'influència corresponents als finals de les línies. L'opció bàsica és la forma rodona, tal com correspon al concepte d'àrea definida per una distància constant a tots els punts de la línia. No obstant, en algunes aplicacions pot resultar més útil que la forma de l'extrem de l'àrea d'influència sigui plana en el punt final de la línia.
Àrees d'influència de múltiples corones
Les àrees d'influència de múltiples corones són opcions que proporcionen alguns programes de SIG per a calcular simultàniament, en una sola execució, una sèrie d'àrees d'influència corresponents a intervals de distàncies successius, que solen anomenar-se corones. Hi ha dues opcions d'àrees d'influència de múltiples corones: corones concèntriques i corones apilades.
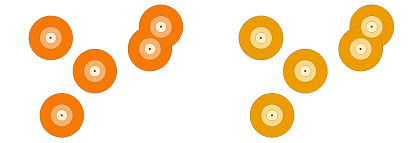
Corones concèntriques
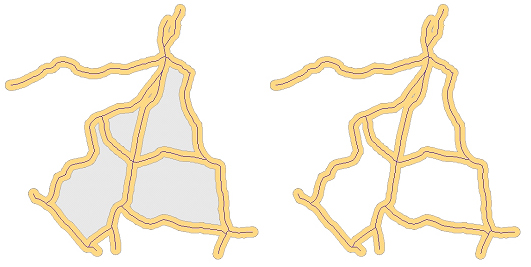
En el cas de les corones concèntriques, cada corona exclou les successives corones que conté. Per exemple, en el cas de tres corones de 0 a 100, de 100 a 200 i de 200 a 300 m a l'entorn d'un punt, cada interval de distància, i l'àrea d'influència corresponent, exclou l'interval de distància anterior. El resultat és equivalent a calcular les àrees de distància de cada interval de distància per separat i superposar-les després mitjançant intersecció, per tal que cada àrea d'influència es descompti de la següent.
Corones apilades
En el cas de les corones apilades, cada corona inclou acumulativament les successives corones que conté. Per exemple, en el cas de tres corones de 0 a 100, de 0 a 200 i de 0 a 300 m a l'entorn d'un punt, cada interval de distància, i l'àrea d'influència corresponent, inclou l'interval de distància anterior. El resultat és equivalent a calcular les àrees de distància de cada interval de distància per separat i deixar-les simplement apilades, sense que cada àrea d'influència es descompti de la següent.
Àrees d'influència euclidianes o geodèsiques
Àrees d'influència euclidianes
Les operacions de geoprocessament, en general, i el càlcul d'àrees de distància, en particular, se solen efectuar amb dades espacials que han estat georeferenciades prèviament segons un sistema de referència espacial de coordenades planes corresponent a una determinada projecció cartogràfica, de manera que totes les operacions geomètriques tenen lloc assumint un pla ideal i, en concret, i pel que fa a les operacions de distància, les propietats i fórmules de càlcul de la distància euclídia. En aquest sentit, es parla doncs d'àrees d'influència euclidianes.
Àrees d'influència geodèsiques
Tanmateix, en determinats casos, sobretot quan l'àrea geogràfica d'interès cobreix una extensió contintental o global, és necessari calcular les operacions de distància segons la distància geodèsica; és a dir, sobre la superfície esfèrica del globus i generar les àrees de distància en coordenades geogràfiques, de manera que es puguin visualitzar adequadament d'acord amb la projecció cartogràfica aplicada en cada moment. En aquest sentit, es parla d'àrees d'influència geodèsiques. No tots els programes de SIG ofereixen l'opció de realitzar operacions d'anàlisi espacial basades en la distància geodèsica.
Anàlisi d'àrees d'influència ràster
L'operació ràster que genera directament àrees d'influència és la dilatació, la qual expandeix una cel·la o un grup de cel·les, de valor diferent al valor de fons del ràster, afegint un determinat nombre de cel·les al voltant de la cel·la o grup de cel·les origen. Tenint en compte que en el model de dades ràster la longitud del costat de la cel·la d'un ràster és fixa i coneguda, l'àrea d'influència s'obté aplicant una dilatació d'un nombre de cel·les igual a la distància desitjada dividida pel costat de la cel·la o resolució espacial del ràster.
Alguns programes de SIG implementen aquesta operació, però la dilatació, de fet, no és una operació pròpia dels SIG, sinó que, juntament amb l'erosió, l'obertura i el tancament, forma part dels operadors bàsics de morfologia matemàtica (Serra, 1982), que tenen aplicacions, entre d'altres en el processament d'imatges.
Anàlisi de distància euclidiana
En la majoria de programes de SIG, l'àrea d'influència en dades ràster s'aconsegueix calculant primer un ràster de distància contínua a partir de les cel·les d'interès i seleccionant posteriorment les cel·les amb valor inferior o igual a la distància desitjada.
Tret de les limitacions a causa de la major o menor resolució espacial de les dades ràster i del fet que en els ràsters la distància es calcula entre centres de cel·la però l'assignació es fa per cel·les senceres, cosa que comporta una certa sobreestimació de la distància en unes cel·les i una subestimació en d'altres, l'anàlisi de distància euclidiana ràster produeix resultats conceptualment equivalents a l'operació vectorial que genera àrees d'influència a l'entorn d'elements geomètrics.
Temes relacionats
- Model de dades ràster
- Model de dades vectorial
- Polígons de Thiessen
- Sistema de referència espacial
- Sistema d’informació geogràfica
Referències
McHarg, I.L. (1969) Design with Nature, New York: Natural History Press.
Serra, J. (1982) Image Analysis and Mathematical Morphology. Oxford: Academic Press.
Sinton, D.F. and Steinitz, C.F. (1969) GRID: A user's manual, Cambridge, Massachussets: Laboratory for Computer Graphics and Spatial Analysis, Graduate School of Design, Harvard University.
Tomlin, C.D. (1980) The Map Analysis Package. Connecticut: Yale School of Forestry and Environmental Studies.
Tomlinson, R.F. (1967) An Introduction to the Geographic Information System of the Canada Land Inventory. Ottawa: Department of Forestry and Rural Development.
Tomlinson, R.F. (1980) "Tha handling of data for natural resources development" in Proceedings of Workshop on Information Requirements for Dvelopment Planning in Developing Countries. Enschede: ITC.
Tomlinson, R.F.; Calkins, H.W. and Marble, D.F. (1976) Computer handling of geographical data. Geneva: UNESCO.
Lectures recomanades
Tomlinson, R.F. (1980) "Tha handling of data for natural resources development" in Proceedings of Workshop on Information Requirements for Development Planning in Developing Countries. Enschede: ITC.

 Contacte
Contacte