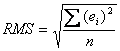Autor: Dr. Joan Nunes. Universitat Autònoma de Barcelona
Promotor: Institut Cartogràfic de Catalunya, 2013
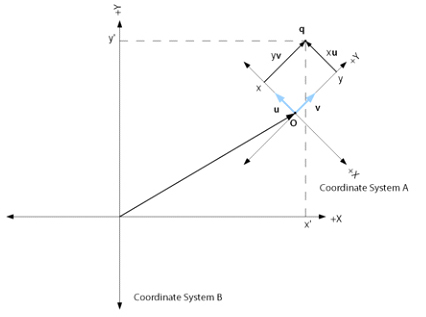
Una transformació de coordenades és la conversió de les coordenades d'un sistema de coordenades a un altre. En el context específic dels sistemes d'informació geogràfica (SIG), la transformació de coordenades és l'operació que converteix les coordenades que defineixen els elements espacials d'un conjunt de dades vectorial, o la posició de les cel·les d'un conjunt de dades ràster, d'un sistema de coordenades a un altre. En particular, en els SIG s'utilitzen transformacions entre sistemes de coordenades cartesianes, generalment en dues dimensions, ja que aquestes són el tipus de coordenades més emprades per a la informació geoespacial.
Les transformacions de coordenades són fonamentals per a la georeferenciació de les dades espacials vectorials o ràster, la correcció geomètrica d'imatges i l'ajust espacial entre conjunts de dades geoespacials. Les transformacions de coordenades intervenen en el procés de digitalització, per tal de traslladar les posicions de l'espai del document a l'espai geogràfic, i també en les operacions de consulta espacial, per a convertir les posicions introduïdes interactivament a la pantalla a posicions geogràfiques.
Sumari:
- Origen
- Definició
2.1 Projeccions cartogràfiques vs transformacions de coordenades en el pla
2.2 Funcions polinòmiques de transformació de coordenades
2.3 Punts de control
2.4 Càlcul de les funcions de transformació per ajust de mínims quadrats
2.5 Mesura de l'error de la transformació: l'error quadràtic mitjà - Transformacions de coordenades en el pla
3.1 Transformacions bàsiques
3.2 Transformació ortogonal o de Helmert
3.3 Transformació afí - Transformació projectiva
- Transformacions polinòmiques no lineals
- Aplicacions en els sistemes d'informació geogràfica
6.1 Calibratge de taules de digitalitzar
6.2 Correcció geomètrica i georeferenciació d'imatges
6.3 Canvi de sistema de coordenades
6.4 Ajust espacial - Temes relacionats
- Referències
- Lectures recomanades
Origen
El concepte de transformació de coordenades és inherent al de sistema de coordenades i, en particular, al de sistema de coordenades cartesianes, establert al segle XVII per René Descartes i desenvolupat entre d'altres per Galileo, Newton i Leibniz, que constitueix el fonament de la geometria analítica i del tractament algebraic de la geometria euclidiana. Posteriorment s'han desenvolupat molts altres sistemes de coordenades entre els quals, les coordenades polars, les coordenades esfèriques o les cilíndriques.
En el context digital, la programació de mètodes numèrics de construcció i anàlisi geomètrica, entre els quals les transformacions de coordenades, constitueix l'anomenada geometria computacional, que data de finals de la dècada de 1960 i principis de la dècada de 1970 (Forrest, 1971). Molts dels mètodes de la geometria computacional (Preparata and Shamos, 1985) sorgiren en resposta a les necessitats de desenvolupament dels gràfics per ordinador i del disseny assistit per ordinador i serien adoptats pels sistemes d'informació geogràfica des dels seus inicis (Tomlinson, 1967).
Definició
Projeccions cartogràfiques vs transformacions de coordenades en el pla
Segons la definició general del concepte, una transformació de coordenades converteix coordenades entre dos sistemes de coordenades qualssevol, en espais de qualsevol nombre de dimensions. Per exemple, la transformació de coordenades polars a cartesianes o de coordenades esfèriques a cartesianes. Tanmateix en el context de la informació geoespacial, es distingeixen tres tipus de transformacions:
- la conversió de coordenades geogràfiques, esfèriques, a coordenades cartesianes, que és l'objecte d'una determinada projecció cartogràfica, mitjançant la funció matemàtica corresponent, i que inclou també la conversió contrària, de coordenades cartesianes a geogràfiques, mitjançant la funció inversa de la projecció cartogràfica.
- la conversió de les coordenades cartesianes resultants d'una projecció cartogràfica a les coordenades cartesianes resultants d'una altra projecció cartogràfica, que constitueix un canvi de projecció cartogràfica, o en termes més generals un canvi de sistema de referència espacial per canvi de projecció, de dàtum o de sistema de coordenades, i que es resol com un procés doble de transformació, de les coordenades cartesianes originals a geogràfiques (projecció inversa o desprojecció) i de coordenades geogràfiques a les noves coordenades cartesianes (reprojecció). mitjançant l'aplicació de les funcions corresponents a les projeccions cartogràfiques implicades.
- la conversió de coordenades cartesianes segons un sistema de coordenades a coordenades cartesianes segons un altre sistema de coordenades, sense implicar un canvi de projecció cartogràfica o quan es desconeix la projecció cartogràfica original, que constitueix l'objecte del que en els sistemes d'informació geogràfica es considera pròpiament una transformació de coordenades.
En els sistemes d'informació geogràfica, doncs, es distingeix entre les transformacions en què intervé una projecció cartogràfica i les transformacions entre sistemes de coordenades cartesianes, generalment en dues dimensions, és a dir en el pla. Les primeres (projecció o canvi de projecció) es resolen mitjançant l'aplicació de les funcions matemàtiques ben definides de les projeccions cartogràfiques corresponents, mentre que les segones (transformacions de coordenades en el pla) es resolen determinant primer la funció de transformació necessària entre els dos sistemes de coordenades cartesianes en el pla i aplicant-la després al conjunt de coordenades a transformar.
Funcions polinòmiques de transformació de coordenades
Les transformacions de coordenades en el pla, o entre diferents plans, constitueixen pròpiament l'objecte de les operacions de transformació de coordenades en els sistemes d'informació geogràfica. En aquest cas, tot i que existeixen un cert nombre de transformacions bàsiques teòriques o funcions primitives, la casuística de transformació és tal que la funció o funcions de transformació particulars en cada cas són desconegudes a priori i cal determinar-les com a primer pas del procés de transformació de coordenades.
Així, el procés general de transformació de coordenades cartesianes consisteix a determinar les funcions F i G (tantes com nombre de coordenades, dues en el cas de transformacions en el pla) que permetin calcular les coordenades finals (x',y') que corresponen a les coordenades inicials (x,y):
x' = F (x,y)
y' = G (x,y)
En les transformacions de coordenades en el pla, o entre diferents plans, les funcions de transformació F i G es plantegen com a funcions polinòmiques, que poden ser de primer grau o de graus superiors. En el cas d'emprar funcions polinòmiques de primer grau, les coordenades de destinació s'obtenen com a combinació lineal de les coordenades originals mitjançant equacions de primer grau, com les següents:
x' = Ax + By + C
y' = Dx + Ey + F
En el cas general d'equacions de primer grau com les anteriors, que corresponen a la transformació afí en el pla, el nombre de paràmetres a determinar o a conèixer per poder formular les equacions d'una determinada transformació i poder aplicar-la són sis, tants com el nombre de coeficients que apareixen en el conjunt d'equacions. Per aquest motiu, les equacions sovint s'anomenen pel nombre de paràmetres que cal conèixer per a efectuar la transformació. Així, per exemple, la transformació afí s'anomena també transformació de sis paràmetres o la transformació ortogonal s'anomena transformació de quatre paràmetres.
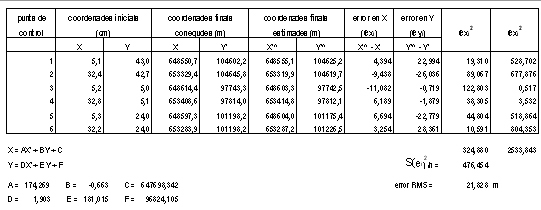
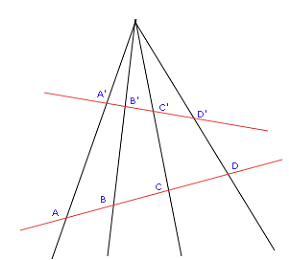
Per a determinar els paràmetres o els coeficients dels polinomis de les equacions de transformació es requereix un nombre igual de valors coneguts. Aquests valors els proporcionen els anomenats punts de control, que són punts dels quals es coneixen les coordenades en el sistema de coordenades inicial i en el sistema de coordenades final, de manera que permeten establir la correspondència entre els dos espais de coordenades i calcular els coeficients dels polinomis de transformació introduint-ne els valors de les coordenades en les fórmules de les equacions. Els punts de control, també anomenats punts de suport, són punts identificables en una imatge, en un mapa analògic o digital o sobre el terreny, de posició coneguda en els dos sistemes de coordenades entre els quals té lloc la transformació. En el cas de les imatges solen ser punts fàcils d'identificar alhora sobre la imatge i sobre un mapa de referència que proporcioni les coordenades finals georeferenciades, com és ara cruïlles de carreteres, colzes de camins, cantonades d'edificis singulars, antenes de comunicacions, etc. En el cas de mapes escanejats o de mapes en paper a digitalitzar, els punts de control solen ser els punts de la quadrícula del sistema de coordenades derivat de la projecció emprada que solen aparèixer impresos en el mapa.
En les transformacions entre sistemes de coordenades bidimensionals, en el pla, cada punt de control consta de dues coordenades, de manera que el nombre de punts de control necessari per a calcular els paràmetres o coeficients de les equacions de transformació és la meitat que el nombre de paràmetres o de coeficients de les equacions de transformació. Així, per exemple, cal un mínim de tres punts de control per a determinar les equacions d'una transformació afí en el pla, dos punts de control en el cas de la transformació ortogonal, o quatre en el cas de la transformació projectiva.
En general, per a transformacions de coordenades resoltes mitjançant funcions polinòmiques de primer grau, el nombre de punts de control és igual al nombre de paràmetres o coeficients de les funcions de transformació dividit pel nombre de dimensions de les coordenades.
Càlcul de les funcions de transformació per ajust de mínims quadrats
L'ús del nombre mínim de punts de control necessaris per a determinar els coeficients de les equacions de transformació proporciona el que s'anomena una solució "exacta" al problema de càlcul dels coeficients. És a dir, una solució que seria vàlida només en el supòsit de tenir la certesa absoluta que els valors de les coordenades inicials i finals de tots i cada un dels punts de control.són exactes al cent per cent, sense gens d'error. Aquest supòsit és materialment impossible d'acomplir en cap aplicació pràctica, ja que tant les coordenades inicials com les finals són valors mesurats i tot mesurament té un cert grau d'error per acurat que sigui.
Conseqüentment, en lloc de determinar els coeficients de les equacions de transformació de coordenades utilitzant el nombre mínim de punts de control necessaris per a cada tipus de funcions de transformació, s'utilitza un excés de punts de control i els coeficients de les equacions es determinen mitjançant un ajust de mínims quadrats, o anàlisi de regressió, prenent les coordenades finals com a variables dependents i les coordenades inicials com a variables independents.
El nombre de punts de control necessaris per a determinar els coeficients de les equacions d'un determinat tipus de transformació polinòmica de primer grau ha de ser com a mínim igual al nombre mínim de punts de control que requereix la transformació més un. Per exemple, quatre punts de control o més en el cas de la transformació afí, tres o més en el cas de la transformació ortogonal, o cinc o més en el cas de la transformació projectiva.
Mesura de l'error de la transformació: l'error quadràtic mitjà
El càlcul de les funcions de transformació per ajust de mínims quadrats, a més de proporcionar una solució més versemblant que la solució "exacta", té l'avantatge addicional de permetre conèixer el grau d'error comès en la transformació de coordenades com a conseqüència de l'error de mesurament de les coordenades dels punts de control i per tant avaluar si la transformació és satisfactòria o bé cal substituir alguns o tots els punts de control per altres de més precisos.
La mesura o estimador global de l'error de la transformació és l'anomenat error quadràtic mitjà, o error RMS (de l'anglès Root Mean Squared Error), que és l'àrrel quadrada del promig dels quadrats dels errors o residus individuals de l'estimació de cada coordenada x o y, segons l'expressió següent:
on
ei és l'error individual d'estimació de cada coordenada x o y, definit com el residu o diferència entre la x coneguda i la x estimada per la funció de transformació (o entre la y coneguda i la y estimada) de cada punt de control.
n és el nombre de punts de control emprats en l'estimació.
Les unitats de l'error RMS són les mateixes que les del sistema de coordenades final. Per exemple, metres en el cas de georeferenciar amb coordenades UTM. El valor de l'error RMS ha de ser tan baix com sigui possible. En tot cas, ha de ser inferior o de l'ordre de l'error comés en el mesurament de les coordenades (precisió) per tal que sigui acceptable. A l'exemple anterior, que correspon al calibratge de la taula de digitalitzar per a la digitalització d'un mapa en paper a escala 1:50000 en el sistema de coordenades planes estatals emprat als Estats Units d'Amèrica, l'error RMS de 21,828 m sobre el terreny és acceptable ja que a l'escala del document a digitalitzar correspon a un error de 0,4 mm sobre el paper, que és de l'ordre de l'error comès per l'ull humà a l'hora d'apreciar i resseguir els traços sobre el paper a digitalitzar.
Tot i les diferències de funcionament, els programes de SIG i de CAD treballen amb excés de coordenades i calculen la transformació més acurada possible per ajust de mínims quadrats amb el nombre de punts de control introduïts o bé donen a triar entre les transformacions que es poden efectuar amb el nombre de punts de control introduïts. Tots els programes informen de l'error RMS i demanen confirmació abans d'aplicar la transformació. Alguns informen de l'error individual (ei) de cada coordenada de cada punt de control per tal de poder descartar aquells punts de control que introdueixin massa error, sempre que quedi un nombre suficient de punts de control, o bé remesurar-los o substituir-los per altres. La manera d'indicar els punts de control varia d'un programa a l'altre, però la majoria permeten introduir-los tant de forma interactiva com per mitjà de llistes de correspondència entre coordenades inicials i finals.
Transformacions de coordenades en el pla
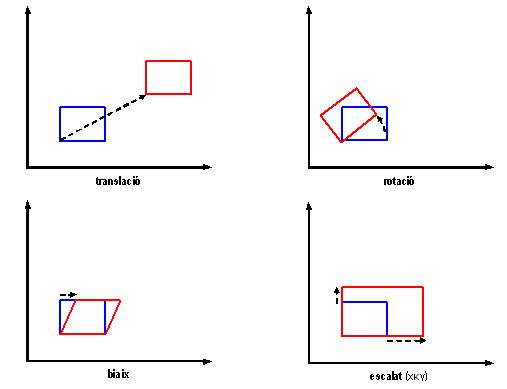
Les transformacions de coordenades en el pla són transformacions en què les coordenades finals s'obtenen com a combinació lineal de les coordenades inicials. És a dir, mitjançant funcions polinòmiques de primer grau. Des del punt de vista de la geometria descriptiva, no analítica, les transformacions de coordenades en el pla s'obtenen totes com a combinacions de les quatre transformacions bàsiques, que són la translació, la rotació, el biaix i l'escalat. El que diferència els diversos tipus de transformacions de coordenades en el pla és la combinació particular d'aquestes transformacions bàsiques en cada tipus de transformació.
Les transformacions bàsiques en el pla són la translació, la rotació, el biaix i l'escalat. Combinades, aquestes quatre transformacions donen lloc a qualsevol transformació lineal, també anomenada transformació de primer grau o transformació de primer ordre.
Translació
La translació és la transformació de coordenades en el pla que consisteix a desplaçar els eixos de coordenades una certa distància, igual o diferent en tots dos eixos, respecte del punt origen de coordenades inicial, la qual cosa és equivalent a un desplaçament del punt de coordenades en un o tots dos eixos. En termes analítics, les noves coordenades s'obtenen com a resultat de sumar una constant igual o diferent a cada coordenada. Per aquest motiu, tota translació comprèn en realitat dues translacions i es determina generalment per mitjà de dos paràmetres de translació, un en x i un altre en y, tret dels casos particulars en que el desplaçament sigui igual en tots dos eixos i només calgui un paràmetre de translació.
Rotació
La rotació és la transformació de coordenades en el pla consistent a girar en un cert angle els eixos de coordenades o, el que és el mateix a girar en un cert angle les figures a transformar. En termes analítics, la rotació s'obté com a resultat de multiplicar la coordenada x pel cosinus de l'angle de rotació i la coordenada y pel sinus del mateix angle. La rotació es determina completament per mitjà d'un únic paràmetre, l'angle de rotació.
Biaix
El biaix és la transformació de coordenades en el pla que consisteix a girar en un cert angle un dels dos eixos de coordenades perquè resultin ortogonals, o deixin de ser-ho en cas que ja fossin ortogonals. Analíticament, el biaix s'obté com a resultat de multiplicar la coordenada y per la tangent de l'angle de l'eix y respecte de l'eix x. El biaix es determina completament per mitjà d'un únic paràmetre, l'angle de rotació de l'eix y respecte de la seva orientació inicial.
Escalat
L'escalat és la transformació de coordenades en el pla que consisteix en l'augment o la disminució proporcional dels valors de les coordenades en un o més eixos. En termes analítics, l'escalat s'obté com a resultat de multiplicar cada coordenada per un factor d'augment o de disminució igual o diferent en cada eix. L'escalat es determina per mitjà de dos paràmetres o bé un de sol, segons que sigui igual o diferent en cada eix.
Transformació ortogonal o de Helmert
La transformació de Helmert en el pla, anomenada també transformació ortogonal o transformació de similitud, és una transformació de coordenades en el pla que combina les transformacions bàsiques de rotació, escalat i translació i que permet obtenir les coordenades finals com a combinació lineal de les coordenades originals dels punts dels elements que són objecte de la transformació.
Concretament, la transformació de Helmert en el pla és un cas particular de transformació afí en el pla, en el qual només s'aplica una translació en x, una translació en y, una rotació i un escalat igual en tots dos eixos. La transformació de Helmert no inclou cap operació de biaix, ja que assumeix que els eixos de coordenades inicials ja són ortogonals i en conseqüència els eixos finals també. Per tant, la transformació de Helmert en el pla tan sols corregeix l'orientació dels eixos, el desplaçament de l'origen de coordenades i el canvi d'unitats de mesura, assumint que els eixos de coordenades originals són ortogonals i que no hi ha deformacions d'escala diferents en x i en y. En aquest sentit, la transformació de Helmert en el pla és la transformació de coordenades en dues dimensions més simple i no pot corregir deformacions de la geometria dels objectes. Serveix només per a transformar coordenades cartesianes que ja són geomètricament correctes a un altre sistema de coordenades cartesianes. Per exemple, un canvi d'origen de coordenades, un canvi d'orientació dels eixos, un canvi d'unitats de mesura o la combinació de tots tres.
En el cas de la transformació de Helmert en el pla, les equacions generals de la transformació de coordenades lineal o de primer grau
x' = Ax + By + C
y' = Dx + Ey + F
esdevenen
x' = Ax + By + C
y' = -Bx + Ay + F
ja que l'escalat es uniforme en les dues direccions, i els quatre coeficients necessaris s'obtenen a partir de les transformacions bàsiques de translació, rotació i escalat de la següent manera:
A = s · cos t
B = s · sin t
C és directament la translació en la direcció x
F és directament la translació en la direcció y
on
s és el factor d'escalat, igual en les direccions x i y
t és l'angle de rotació, mesurat en sentit antihorari a partir de l'eix x
La transformació de Helmert en el pla es determina, doncs, per mitjà de quatre paràmetres (dues translacions, una rotació i un escalat; o bé els quatre coeficients de les equacions de transformació) i requereix només dos punts de control per a obtenir la solució "exacta". Per aquest motiu es coneix també com a transformació de quatre paràmetres. Tanmateix, per poder estimar l'error de transformació comès com a conseqüència dels errors en el mesurament dels punts de control, els coeficients de les equacions de la transformació ortogonal es calculen per ajust per mínims quadrats utilitzant tres o més punts de control.
La transformació de Helmert en tres dimensions requereix set paràmetres, i com a tal es coneix també com a transformació de set paràmetres, i s'utilitza en geodèsia per a obtenir equacions de transformació entre dàtums diferents.
La transformació afí en el pla és el cas general de transformació lineal de coordenades en el pla i s'obté com a combinació de dues translacions (una en x i una en y), una rotació, un biaix i dos escalats diferents en x i en y. En aquest sentit, i a diferència de la transformació de Helmert, la transformació afí en el pla pot corregir deformacions de la geometria dels objectes a transformar derivades de la no perpendicularitat dels eixos de coordenades originals i d'estiraments diferents en les dues direccions. Per aquest motiu s'utilitza per a la correcció geomètrica d'imatges i la transformació de coordenades d'elements vectorials quan no es té la certesa que les coordenades originals siguin geomètricament correctes. Per exemple, en el cas de mapes en paper que poden haver sofert deformacions per l'alteració física del suport material o com a conseqüència de la reproducció amb mitjans poc acurats, com és ara fotocopiadores.
Les equacions de la transformació afí en el pla són les equacions generals de la transformació de coordenades lineal o de primer grau:
x' = Ax + By + C
y' = Dx + Ey + F
i s'obtenen a partir de les transformacions bàsiques de translació, rotació, biaix i escalat independent en x i en y de la següent manera:
A = sx · cos t
B = sy · (k · cos t - sin t)
D = sx · sin t
E = sy · (k · sin t + cos t)
C és directament la translació en la direcció x
F és directament la translació en la direcció y
on
sx és el factor d'escalat en la direcció x
sy és el factor d'escalat en la direcció y
t és l'angle de rotació, mesurat en sentit antihorari a partir de l'eix x
k és el factor de biaix, igual a la tangent de l'angle de l'eix y respecte de l'eix x en l'original
La transformació afí en el pla es determina, doncs, per mitjà de sis paràmetres (dues translacions, una rotació, un biaix i dos escalats; o bé els sis coeficients de les equacions de transformació) i requereix tres punts de control per a obtenir la solució "exacta". Per aquest motiu es coneix també com a transformació de sis paràmetres. Tanmateix, per poder estimar l'error de transformació comès com a conseqüència dels errors en el mesurament dels punts de control, els coeficients de les equacions de la transformació afí es calculen per ajust per mínims quadrats utilitzant quatre o més punts de control.
Transformació projectiva
La transformació projectiva, anomenada també homografia, és una transformació lineal de coordenades entre dos plans diferents, de manera que els eixos de coordenades del sistema de coordenades final són la projecció sobre un pla diferent, més altres transformacions en el pla com és ara rotació, translació, biaix o escalat, dels eixos de coordenades del sistema de coordenades inicial.
La transformació projectiva s'utilitza, entre d'altres aplicacions, per a la correcció geomètrica i georeferenciació de fotografies aèries verticals, sempre que les fotografies hagin estat preses a gran alçada, corresponguin a terrenys de superfície essencialment plana i s'aprofiti només la part central dels fotogrames o imatges, allà on la verticalitat de la càmera és màxima, de manera que es puguin negligir els efectes del relleu en la distorsió de la imatge captada. En altres condicions, menys favorables, cal emprar transformacions de coordenades més complexes en tres dimensions, com és ara l'ortorectificació d'imatges, en les quals intervé l'altitud del relleu com a coordenada z.
Les equacions de la transformació projectiva entre dos plans són les següents:
x’ = (Ax + By + C) / (Gx + Hy + 1)
y’ = (Dx + Ey + F) / (Gx + Hy + 1)
La transformació projectiva és més complexa que la transformació afí i no se solen interpretar els coeficients de les equacions en termes de transformacions bàsiques, simplement es calculen a partir dels valors de les coordenades inicials i finals dels punts de control. El nombre de coeficients a calcular per a determinar les equacions d'una transformació projectiva és de vuit coeficients o paràmetres i per tant es requereixen quatre punts de control per a la solució "exacta" i cinc o més punts de control per al càlcul mitjançant ajust de mínims quadrats que permet conèixer l'error RMS de la transformació. Per aquest motiu, la transformació projectiva es coneix també com a transformació de vuit paràmetres.
Transformacions polinòmiques no lineals
És possible realitzar transformacions de coordenades utilitzant polinomis de grau superior a 1. En aquests casos, les transformacions s'anomenen quadràtica (grau 2), cúbica (grau 3), etc. En general, les transformacions de grau superior són més precises, amb un error RMS més baix, que les de grau inferior, si bé en molts casos el guany de precisió aconseguit amb polinomis de grau superior és marginal respecte a l’aconseguit amb polinomis de primer grau i no compensa l'augment de complexitat i de punts de control que es requereixen per a calcular les equacions de transformació de graus superiors.
El procediment general de càlcul és el mateix en tots els casos, els coeficients de les equacions es calculen per ajust de mínims quadrats utilitzant un excés de punts de control respecte del nombre mínim requerit per a calcular els coeficients de les equacions de forma "exacta", sense estimació de l'error de la transformació.
A tall d'exemple, les equacions per a una transformació de coordenades polinòmica de segon grau en dues dimensions, o transformació quadràtica, serien les següents
x' = A x + B y + C x2 + D x y + E y2 + F
y' = G x + H y + I x2 + J x y + K y2 + L
És a dir, un total de dotze coeficients o paràmetres a determinar, que requereixen un mínim de sis punts de control per a obtenir la solució exacta i set o més punts de control per a realitzar el càlcul per ajust de mínims quadrats amb estimació de l'error RMS de la transformació.
Un cas concret de transformació polinòmica no lineal és la transformació quíntica, de grau 5, que s'utilitza per a realitzar la transformació de coordenades coneguda com deformació elàstica, emprada per a l'ajust espacial entre elements de diferents conjunts de dades.
Les transformacions polinòmiques no lineals s'utilitzen només en aplicacions que requereixen nivells d'error molt baixos i, tret de casos específics com la deformació elàstica, rarament se solen utilitzar polinomis de grau superior a la transformació quadràtica o cúbica.
Aplicacions en els sistemes d'informació geogràfica
Les transformacions de coordenades s'utilitzen en els sistemes d'informació geogràfica amb finalitats diverses relacionades amb la georeferenciació de les dades espacials, bé directament amb la finalitat explícita de georeferenciar un conjunt de dades geoespacials o bé indirectament amb la finalitat de canviar el sistema de coordenades o modificar la forma de dades espacials ja georeferenciades per tal de corregir-ne la geometria. Entre les principals aplicacions de les transformacions de coordenades que tenen per finalitat la georeferenciació de dades espacials hi ha el calibratge de taules de digitalitzar i la correcció geomètrica i georeferenciació d'imatges. Entre les segones hi ha el canvi de sistema de coordenades i l'ajust espacial.
Calibratge de taules de digitalitzar
En la digitalització manual, mitjançant taula de digitalitzar, el calibratge de la taula de digitalitzar serveix per a definir la transformació de coordenades que el programa de digitalització haurà d'aplicar a les coordenades de cada punt introduït per mitjà de la taula per tal de transformar les coordenades locals del dispositiu, mesurades en mil·límetres o polzades respecte a la cantonada inferior esquerra de l'àrea activa de la taula, a coordenades georeferenciades, mesurades en metres o altres unitats sobre el terreny, segons la projecció i sistema de coordenades del mapa en paper que s'està digitalitzant.
Per a calibrar la taula de digitalitzar i definir la transformació de coordenades que permetrà georeferenciar les dades a mesura que es van digitalitzant cal indicar punts de control, marcant-los sobre el document en paper fixat a la taula i introduint les coordenades georeferenciades corresponents. Generalment els programes de digitalització informen de l'error RMS de la transformació resultant del calibratge de la taula prèviament a procedir amb la digitalització, per si no es considera acceptable i es prefereix recalibrar la taula introduint de nou els punts de control o substituint-los per altres de més acurats. Hi ha programes, però, que només enregistren els punts de control, efectuen la digitalització en coordenades de dispositiu i apliquen després la transformació de coordenades definida pels punts de control informant de l'error RMS de la transformació al final del procés.
La transformació de coordenades més emprada en el calibratge de taules de digitalitzar és la transformació afí, encara que de vegades, si l'original no presenta deformacions substancials, també s'utilitza la transformació ortogonal.
Correcció geomètrica i georeferenciació d'imatges
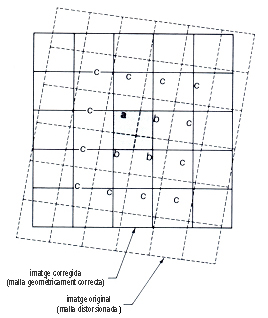
Les dades ràster i en general les imatges s'obtenen generalment sense georeferenciar perquè els dispositius de captació de dades, ja siguin escàners per a convertir imatges analògiques en imatges digital o sensors digitals transportats per satèl·lits o aerotransportats, no són capaços de georeferenciar les imatges perquè no disposen de la informació de punts de control necessària ni tenen incorporats els algorismes de càlcul corresponents.
Per a la georeferenciació d'imatges i ràsters cal efectuar també una transformació de coordenades mitjançant punts de control, que fan correspondre punts de la imatge a punts de coordenades conegudes, però en aquest cas la transformació de coordenades té també una finalitat de correcció geomèrica perquè ha de restablir la geometria regular de la malla ràster, distorsionada en la imatge captada, i donar-li l'orientació correcta. A més, la georeferenciació d'imatges i ràsters implica també recalcular els valors que correspondran a les noves posicions de les cel·les un cop feta la correcció, procés que s'anomena remostreig del ràster o imatge i que és una interpolació de valors.
Les transformacions de coordenades més emprades en les aplicacions habituals de georeferenciació de dades ràster i imatges, com és ara la georeferenciació de mapes escanejats o la correcció geomètrica d'imatges de satèl·lit, són les transformacions polinòmiques de primer o de segon grau, ja que tant en un cas com en l'altre es poden assumir superfícies essencialment planes, bé perquè l'original en paper ja és un mapa amb una projecció cartogràfica, bé perquè l'altitud a què es capten les imatges de satèl·lit és molt gran. No obstant, per a aplicacions més acurades s'utilitzen la transformació projectiva i, especialment, les transformacions en tres dimensions, com és ara l'ortorectificació de fotografies aèries per a produir ortofotomapes, en la qual intervé també l'altitud del relleu com a coordenada z mitjançant models digitals d'elevacions detallats i un alt nombre de punts de control.
Canvi de sistema de coordenades
El canvi de sistema de coordenades de dades ja georeferenciades té lloc en casos de canvis d'unitats o translacions que desplacen l'origen de coordenades. En aquests casos les transformacions a aplicar són simples i es poden resoldre de forma exacta proporcionant el nombre mínim de punts de control. Generalment, una transformació ortogonal o afí és suficient.
L'ajust espacial entre elements de conjunts de dades diferents té per finalitat modificar la geometria dels elements d'un conjunt de dades per tal d'adaptar-los i, en la mesura possible, fer-los coincidir amb la geometria dels elements d'un altre conjunt de dades. Aquest tipus de necessitats apareixen en casos en què s'han digitalitzat de manera independent diferents conjunts de dades d'elements coincidents totalment o en part i cal aconseguir amb posterioritat el registre entre els diferents conjunts de dades. També sorgeixen en el cas d'haver de georeferenciar dades espacials de les quals es desconeix el sistema de referència espacial original i es volen georeferenciar i ajustar a un determinat sistema de referència espacial. En alguns casos es recorre també a l'ajust espacial per a transformar les coordenades d'un sistema de referència espacial a un altre, per exemple per a canviar de dàtum, però aquest tipus d'operació és desaconsellable, ja que és preferible efectuar el canvi de projecció cartogràfica i de dàtum, desprojectant i reprojectant de nou les dades.
En general, les transformacions lineals de coordenades en el pla són insuficients per a les aplicacions d'ajust espacial, ja que les deformacions a corregir són múltiples i no sistemàtiques. Una de les transformacions de coordenades més emprades per a l'ajust espacial és l'anomenada deformació elàstica, que es basa en polinomis de cinquè grau.
Temes relacionats
- Digitalització
- Georeferenciació
- Interpolació
- Model digital d'elevacions
- Sistema de referència espacial
- Sistema d'informació geogràfica
Referències
Forrest, A.R. (1971) "Computational geometry", Proc. Royal Society London, 321, series 4, 187-195.
Preparata, F.P. and Shamos, M.I (1985) Computational Geometry - An Introduction. New York: Springer-Verlag.
Tomlinson, R.F. (1967) An Introduction to the Geographic Information System of the Canada Land Inventory. Ottawa: Department of Forestry and Rural Development.
Lectures recomanades
Maling, D.H. (1991) “Coordinate systems and map projections for GIS” in Maguire D.J., Goodchild, M.F. and Rhind D.W. (eds.) Geographical Information Systems: principles and applications. London: Longman.

 Contacte
Contacte