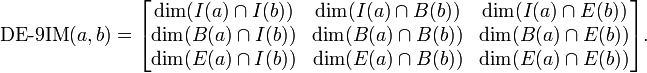Model de nou interseccions estès dimensionalment

Autor: Dr. Joan Nunes. Universitat Autònoma de Barcelona
Promotor: Institut Cartogràfic de Catalunya, 2013

 

El model de nou interseccions estès dimensionalment (DE-9IM, de l'anglès dimensionally extended nine-intersection model) és un model topològic que permet calcular i descriure les relacions espacials entre dos objectes geomètrics en l'espai de dues dimensions.

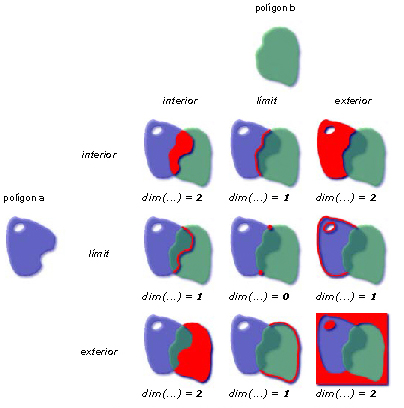
El model de nou interseccions estès dimensionalment DE-9IM es basa en la matriu de 3 x 3 interseccions entre l'interior, el límit i l'exterior dels dos objectes geomètrics. Calculant el resultat de cada una de les nou possibles interseccions entre les parts (interior, límit i exterior) dels dos objectes i determinant la dimensió del resultat (0, 1 o 2, segons que el resultat de la intersecció siguin punts, línies o polígons) és possible caracteritzar la relació espacial entre els dos objectes geomètrics. Per exemple, si la intersecció dels interiors de dos polígons és de dimensió 2, la relació espacial entre els dos polígons és de cavalcament; si la intersecció dels interiors de dues línies és de dimensió 0, la relació espacial entre les dues línies és de creuament (és a dir, comparteixen un punt); etc.

El model de nou interseccions estès dimensionalment DE-9IM ha estat un dels majors avenços en la recerca teòrica sobre informació espacial i bases de dades espacials, ja que és el fonament per a definir predicats espacials que permeten implementar consultes espacials en les bases de dades espacials mitjançant un llenguatge de consulta espacial de tipus declaratiu. En particular, el model de nou interseccions estès dimensionalment DE-9IM ha estat adoptat en l'especificació de l'estàndard Simple Feature Access (SFA) d'emmagatzematge d'objectes espacials en bases de dades per a definir els predicats de consulta espacial del llenguatge de consulta espacial SQL-MM.

 

Origen

El model de nou interseccions estès dimensionalment, per a definir i classificar relacions espacials entre objectes geomètrics de dues dimensions, fou desenvolupat per diversos autors a principis de la dècada de 1990.

Egenhofer desenvolupà primer el model de quatre interseccions (4IM) entre interior i límit dels objectes geomètrics (Egenhofer and Franzosa, 1991), a partir de la topologia algebraica i la teoria de conjunts de punts (Egenhofer and Herring, 1990), i posteriorment el model de nou interseccions (9IM), que incorpora també l'exterior dels objectes geomètrics i que es coneix com matriu d'Egenhofer (Egenhofer et al. 1993; Egenhofer et al., 1994).

Poc després, l'extensió del model de nou interseccions, per part de Clementini i altres autors (Clementini et. al., 1993, 1994, 1996), en el sentit de considerar la dimensió topològica (0, 1, 2) del resultat de les nou interseccions entre interior, límit i exterior dels objectes geomètrics en lloc de limitar-se a valos binaris fals o cert quan el resultat de la intersecció és buit o no, donaria lloc al model de nou interseccions estès dimensionalment (DE-9IM), que també es coneix com matriu de Clementini.

El 1999 Open GIS Consortium (actualment Open Geospatial Consortium, OGC) incorporà el model de nou interseccions estès dimensionalment (DE-9IM) dins de l'especificació de l'estàndard Simple Feature Access (SFA) per a SQL (OGC, 1999), en el que seria la primera implementació de predicats espacials que farien possible la definició d'un llenguatge de consulta espacial i les bases de dades espacials. El 2003 seria adoptat també per ISO/TC 211.

Definició

El model de nou interseccions estès dimensionalment (DE-9IM) entre dos objectes geomètrics es defineix per mitjà de la matriu de 3 x 3 interseccions següent:

 

on
dim( ) és la dimensió més gran de la intersecció (∩) entre l'interior, el límit o l'exterior de l'objecte geomètric a i l'interior, el límit o l'exterior de l'objecte geomètric b
I( )   és l'interior de l'objecte geomètric a o b
B( )  és el límit de l'objecte geomètric a o b
E( )  és l'exterior de l'objecte geomètric a o b

Els conceptes d'interior, límit i exterior dels objectes geomètrics, o geometries com se'n sol dir també, provenen de la topologia algebraica o teoria de conjunts de punts i ofereixen una definició inambigua de les parts topològicament rellevants dels objectes geomètrics en dues dimensions:

• límit: el límit d'un objecte geomètric (element geomètric o geometria) és la regió de l'espai (conjunt d'elements geomètrics o conjunt de geometries, en general conjunt de punts) de dimensió immediatament inferior a la de l'objecte geomètric que fixen els extrems entre els quals estan compresos tots els punts de l'objecte geomètric. El concepte és anàleg al d'extrems d'un interval. Així, en el cas d'un objecte geomètric de tipus punt, que té dimensió 0, el límit és el conjunt buit (dimensió -1); en el cas d'un objecte de tipus línia, que té dimensió 1, el límit són els dos punts extrems (dimensió 0), inicial i final; i en el cas d'un objecte de tipus polígon, que és de dimensió 2, el límit és la línia o línies (dimensió 1) que forma el contorn exterior i possibles contorns interiors, en cas d'haver-hi forats, del polígon.
• interior: l'interior  d'un objecte geomètric (element geomètric o geometria) és la regió de l'espai que resta de l'objecte geomètric quan se n'exclou el límit. El concepte és anàleg al de l''interval obert que resulta d'excloure els extrems d'un interval tancat. Conseqüentment, la dimensió de l'interior d'un objecte geomètric és la mateixa que la de l'objecte. En el cas d'un punt, l'interior és el punt mateix (dimensió 0); en el cas d'una línia, l'interior és el conjunt de punts (dimensió 1) que pertanyen a la línia entre els dos extrems; i en el cas d'un polígon, l'interior és l'àrea (dimensió 2) o conjunt de punts dins del polígon que no pertanyen al contorn.
• exterior: l'exterior d'un objecte geomètric (element geomètric o geometria) és l'univers, la regió de l'espai de dues dimensions que no forma part del límit ni de l'interior de l'objecte geomètric.

En el model de nou interseccions estès dimensionalment (DE-9IM) primer es calcula la intersecció entre cada possible parell de límit, interior i exterior dels dos objectes geomètrics i després es determina la dimensió més gran del resultat de cada intersecció. Els nou valors de dimensió trobats formen la matriu i es denoten per mitjà dels valors {0,1,2,T,F,*}, que signifiquen respectivament:

• 0 : punt, quan l'objecte geomètric de dimensió més gran resultat de la intersecció és un conjunt de punts
• 1 : línia, quan l'objecte geomètric de dimensió més gran resultat de la intersecció és un conjunt de línies
• 2 : àrea, quan l'objecte geomètric de dimensió més gran resultat de la intersecció és un conjunt d'àrees
• T : cert (true, T), valor genèric quan el resultat de la intersecció no és el conjunt buit i pot ser {0,1,2}
• F : fals (false, F), quan el resultat de la intersecció és el conjunt buit
• * : no rellevant, quan el resultat de la intersecció no és rellevant per a definir una relació espacial
       (la relació espacial queda completament determinada per la resta d'interseccions amb valor rellevant)

Els nou valors de dimensió trobats que formen la matriu es poden expressar mitjançant una seqüència de codificació en una sola línia, per exempleT*F**FFF*.Cada relació espacial definida mitjançant el model presenta una seqüència de codificació determinada que constitueix el seu patró característic. Aquests patrons característics s'utilitzen com a definició i valor de comparació per avaluar els predicats espacials en les operacions de consulta espacial. Així, per exemple, en el cas de dos polígons que presenten cavalcament, com els de la figura, la matriu resultant del model és (212101212), mentre que el cas general per a la relació cavalcament entre dos objectes geomètrics de qualsevol dimensió (un punt, línia o polígon respecte a un altre punt, línia o polígon) seria (T*T***T**).

Exemple  de resultat del model de nou interseccions estès dimensionalment (DE-9IM) en el cas de la relació espacial de cavalcament entre dos polígons. La matriu resultant en forma de seqüència de codificació és (212101212). Font: PostGIS Project (2012).

 

Relacions espacials

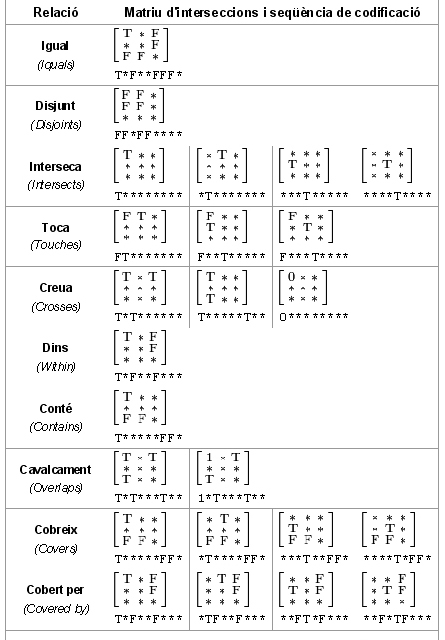
Les relacions espacials que es poden derivar del model DE-9IM, entre dos elements geomètrics qualssevol de dimensió 0, 1 o 2 (punt, línia o polígon), inclouen les següents:

Relacions espacials segons el model DE-9IM. Font: http://en.wikipedia.org/wiki/DE-9IM

Els valors dimensionals concrets de T (i de *) en les matrius de les diferents relacions espacials depenen en cada cas dels elements geomètrics participants a la relació. Els casos possibles són punt amb punt, punt amb línia, punt amb polígon, línia amb punt, línia amb línia, línia amb polígon, polígon amb punt, polígon amb línia i polígon amb polígon.

Predicats de consulta espacial

El model DE-9IM ha permès definir predicats de consulta espacial (per comoditat, predicats espacials) en el llenguatge SQL ampliat per a calcular i retornar com a resultat la seqüència de codificació de la matriu de nou interseccions corresponent a la relació espacial entre dos objectes espacials determinats. Per exemple, la sentència SQL per saber la relació entre els polígons a i b de l'exemple anterior, assumint que pertanyen a una mateixa taula anomenada arees, seria:

El resultat d'aquesta consulta seria la matriu de nou interseccions corresponent a la relació cavalcament entre dos polígons (212101212).

Inversament, es possible efectuar consultes per a determinar quins objectes espacials compleixen una determinada relació. Per exemple, per saber quines carreteres creuen espais naturals, la sentència de SQL ampliat seria:

El nom concret dels operadors espacials en el llenguatge SQL varia segons cada programa de gestió de bases de dades espacials. Per exemple, PostGIS anomena ST_RELATE l'operador RELATE. El model de dades estàndard Simple Feature Access defineix mètodes específics per a cada relació espacial: equals (igual), disjoint (disjunt), intersects (interseca), touches (toca), crosses (creua), within (dins), contains (conté), overlaps (cavalca), més el mètode genèric relate (relaciona) que avalua si la relació espacial entre dos objectes geomètrics és igual a una determinada matriu d'interseccions.

Unió espacial

Una de les capacitats fonamentals dels sistemes de gestió de bases de dades és la possibilitat de realitzar la unió relacional (join) de dues taules en el llenguatge SQL mitjançant una condició que estableixi la correspondència entre columnes de les dues taules, expressada a la clàusula WHERE. Per exemple, per afegir el nom de comarca a cada municipi de la taula municipis, la sentència SQL seria:

De la mateixa manera que es poden relacionar dues taules alfanumèriques per mitjà d'una columna de valors alfanumèrics, en el llenguatge de consulta SQL estès espacialment és possible relacionar dues taules corresponents a dos objectes geomètrics per mitjà d'una condició espacial basada en algun dels predicats de consulta espacial. En aquest cas, es tracta de realitzar el que es coneix com unió espacial (spatial join). Per exemple, per saber quins nuclis urbans pertanyen a cada comarca, en el cas que la taula de nuclis no disposi d'un atribut que indiqui el codi de comarca de cada nucli urbà, la sentència SQL seria:

 

Temes relacionats

• Base de dades espacial
• Simple Feature Access

Referències

Clementini, E.; Di Felice, P. and van Oosterom, P. (1993) "A small set of formal topological relationships suitable for end-user interaction", In Abel, D. and Ooi, B. C. (eds.) Advances in Spatial Databases: Proceedings Third International Symposium, SSD '93 Singapore. Lecture Notes in Computer Science. 692. New York: Springer.

Clementini, E. and Di Felice, P. (1996) "Model for Representing Topological Relationships Between Complex Geometric Features", Spatial Databases.- Information Sciences, 90(1-4),121-136.

Clementini, E.; Sharma, J. and Egenhofer, M. (1994) "Modelling topological spatial relations: Strategies for query processing", Computers & Graphics, 18(6), 815–822.

Egenhofer, M. (1994) "Deriving the composition of binary topological relations", Journal of Visual Languages Computing, 5(2), 133–149.

Egenhofer, M.; Clementini, E. and di Felice, P.A. (1994) "Topological relations between regions with holes", International Journal of Geographical Information Systems, 8(2), 129-142.

Egenhofer, M. and Franzosa, R.D. (1991) "Point-set topological spatial relations", International Journal of Geographical Information Systems, (5)2, 161-174.

Egenhofer, M. and Herring, J. (1990) "A mathematical framework for the definition of topological relationships", Proceedings Fourth International Symposium on Spatial Data Handling Zürich, Switzerland.

Egenhofer, M.; Sharma, J. and Mark, D. (1993) "A Critical Comparison of the 4-Intersection and 9-Intersection Models for Spatial Relations: Formal Analysis", Proceedings of AUTOCARTO 11, Bethesda, Virginia: ASPRS.

ISO/TC211 (2003a) ISO 19107: Geographic information - Spatial schema, Geneva, Switzerland: International Organization for Standardization (ISO)

ISO/TC211 (2003b) ISO 19125: Geographic information - Simple Feature Access (SFA), Geneva, Switzerland: International Organization for Standardization (ISO)

OGC (1999) OpenGIS Simple Features Specification for SQL (Revision 1.1). Wayland, MA: OpenGIS Consortium Inc..

PostGIS Project (2012) PostGIS 2.0.1SVN Manual, Chapter 4.

http://postgis.org/documentation/manual-svn/using_postgis_dbmanagement.html#DE-9IM> [Consulta: 16 maig 2012]

 

Lectures recomanades

Strobl, C. (2008) "Dimensionally Extended Nine-Intersection Model (DE-9IM)" in Shekar, S. and Xiong, H. (eds.) Encyclopedia of GIS, New York: Springer.