Autor: Dr. Joan Nunes. Universitat Autònoma de Barcelona
Promotor: Institut Cartogràfic de Catalunya, 2013
La unió espacial (spatialjoin) és una operació espacial que permet relacionar i combinar les taules d'atributs de dos conjunts d'elements per mitjà de la correspondència entre elements segons una relació espacial determinada. La unió espacial, a diferència de les operacions de geoprocessament, no genera nous elements geomètrics, tan sols estableix la correspondència entre elements dels dos conjunts i combina la informació de les respectives taules d'atributs.
La unió espacial és una operació de relació entre elements, pròpia dels sistemes d’informació geogràfica, anàloga a la unió relacional, però que a diferència d'aquesta estableix la correspondència entre elements per mitjà d'una relació espacial concreta, com és ara intersecció, contenció o proximitat, en lloc de cercar la concordança entre elements en la coincidència o comparació de valors d'atributs comuns.
Sumari:
Origen
La unió espacial és una evolució de l'operació de superposició emprada en geoprocessament. El terme unió espacial (spatial join) apareix a finals de la dècada de 1980 (Aronson, 1987) com a denominació conceptual de tot tipus d'operacions de superposició de mapes; és a dir, d'operacions de interrelació espacial. La operació en si d'unió espacial es desenvolupà en els sistemes d’informació geogràfica a mitjans de la dècada de 1990, en el moment en què aparegueren en el mercat nous tipus de programari de SIG més interactius, com és ara els programes de SIG d'escriptori (Longley, et al.; 2010). En aquesta nova generació de programes de SIG, s'aconseguí una major interactivitat que en els programes de SIG tradicionals emprats fins aleshores, gràcies a la disponibilitat d'algorismes i procediments de selecció espacial interactiva que estalviaven haver de realitzar una operació de superposició i calcular i emmagatzemar nova geometria cada vegada que calia relacionar dues classes d'elements (Laurini and Thompson, 1992).
La unió espacial, en particular, deriva del fet que es pot establir la correspondència entre elements sencers de dos conjunts de dades diferents segons una relació espacial sense haver de calcular la intersecció dels elements dels dos conjunts. Un cop establerta la correspondència, com que es tracta d'elements sencers, es poden associar els elements d'un conjunt als elements de l'altre combinant simplement les taules d'atributs respectives, com si es tractés d'una unió relacional de taules basada en els valors d'atributs comuns.
Posteriorment, a partir del desenvolupament de les bases de dades espacials, l'emmagatzematge de la geometria en taules i la disponibilitat de llenguatges d'interrogació de bases de dades ampliats amb predicats espacials, basats en el model de nou interseccions estès dimensionalment (Clementini et al., 1994), han portat a esborrar progressivament la diferència entre unió relacional i unió espacial en l'àmbit de les bases de dades espacials (Shekhar and Chawla, 2003).
Definició
La unió espacial utilitza relacions espacials per a establir la correspondència entre elements de dos conjunts de dades geoespacials per tal de poder combinar els registres de les taules d'atributs respectives concordants segons la relació espacial emprada.
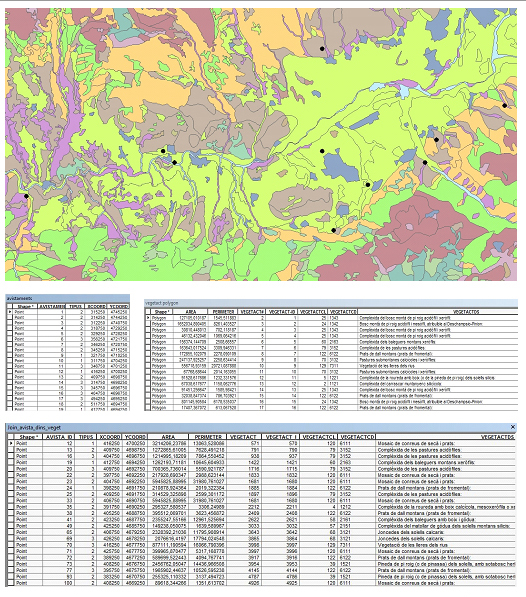
La unió espacial proporciona informació a mig camí entre una selecció espacial i una superposició. Per exemple, donat un conjunt d'elements de tipus polígon que representen espais naturals i un altre conjunt d'elements de tipus polígon que representen termes municipals, la informació proporcionada respectivament per la selecció espacial, la unió espacial i la superposició utilitzant la relació espacial d'intersecció és la següent:
- Selecció espacial: permet obtenir, en forma de selecció, quins municipis intersequen amb algun espai natural, sense especificar quin.
- Unió espacial: permet obtenir, en forma de taula, amb quin(s) espai(s) natural(s) interseca cada municipi i associar a cada municipi els atributs disponibles de cada un dels espais naturals corresponents.
- Superposició: permet obtenir, en forma d'un nou conjunt de dades espacials, cada una de les parts de cada municipi compresa dins de cada un dels espais naturals i saber-ne la superfície.
A diferència de les superposicions de mapes, la unió espacial actua només en aquelles situacions en què l'avaluació de la relació espacial no requereix generar nous elements geomètrics i es pot resoldre com una correspondència entre elements sencers dels dos conjunts de dades, de manera que el resultat es pot presentar com una taula que combina els registres concordants de les respectives taules, anàloga al resultat d'una unió relacional.
Com en el cas de la unió relacional, la relació espacial entre dues classes d'elements donarà lloc a registres concordants en les dues taules i registres no concordants en una o altra de les dues taules. Per tant, a l'hora d'efectuar una unió espacial, seguint la mateixa lògica que la de la unió relacional, es poden plantejar pràcticament els mateixos tipus d'unió de taules. És a dir, la unió espacial interna (inner join), la unió espacial externa esquerra (left outer spatial join) i la unió espacial externa dreta (right outer spatial join):
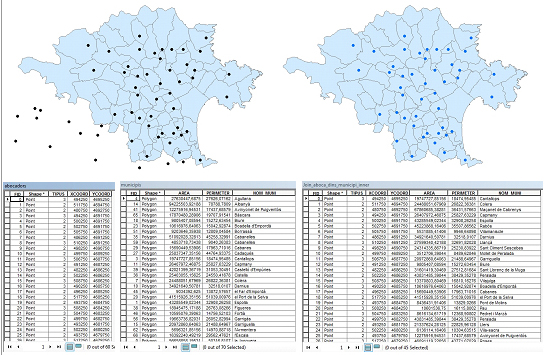
- Unió espacial interna (inner join): el resultat conté només els registres combinats de les taules dels dos conjunts d'elements entre els quals hi ha correspondència segons la relació espacial.
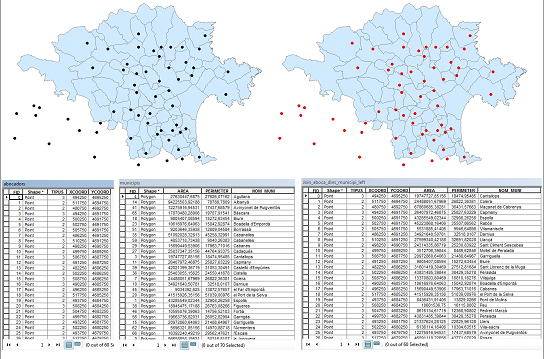
- Unió espacial externa esquerra (left outer spatial join): el resultat conté tots els registres de la taula d'atributs del conjunt d'elements de destinació, amb la informació combinada dels registres de la taula d'atribuits del conjunt d'elements a combinar amb els quals hi ha correspondència segons la relació espacial. Els registres de la taula d'atributs del conjunt d'elements de destinació sense relació espacial amb cap element del conjunt d'elements a combinar tindran valors nuls en els atributs procedents de la taula d'atributs del conjunt d'elements a combinar.
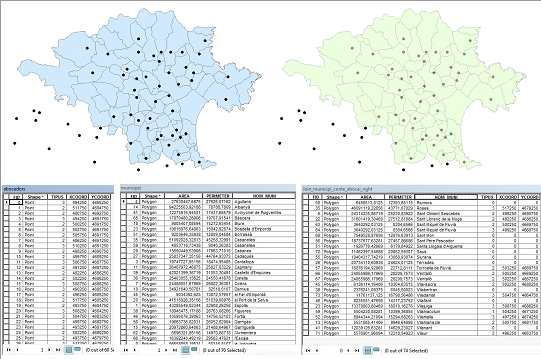
- Unió espacial externa dreta (right outer spatial join): el resultat conté tots els registres de la taula d'atributs del conjunt d'elements a combinar, amb la informació combinada dels registres de la taula d'atribuits del conjunt d'elements a combinar amb els quals hi ha correspondència segons la relació espacial, repetits tantes vegades com elements hi hagi en el conjunt d'elements de destinació que concordin amb cada element a combinar. Els registres de la taula d'atributs del conjunt d'elements a combinar sense relació espacial amb cap element del conjunt d'elements a combinar apareixeran una sola vegada i tindran valors nuls en els atributs procedents de la taula d'atributs del conjunt d'elements de destinació.
La unió espacial interna i la unió espacial externa esquerra serveixen per a relacions 1:1 i M:1 entre el conjunt d'elements de destinació i el conjunt d'elements a combinar. La unió espacial externa dreta serveix per a relacions 1:M entre el conjunt d'elements de destinació i el conjunt d'elements a combinar (o M:1 vista la relació des del costat del conjunt d'elements a combinar).
No tots els programes de SIG implementen l'operació d'unió espacial i no tots els que la implementen ho fan de la mateixa manera.
Els programes de SIG que segueixen una lògica de SIG més clàssica, implementen la unió espacial com una combinació virtual de la taula d'atributs del conjunt d'elements a combinar sobre la taula d'atributs del conjunt d'elements de destinació, de manera que realment no es genera cap nou conjunt d'elements ni s'emmagatzema res físicament. Aquesta implementació només és possible aplicant la unió espacial externa esquerra, que conserva tots els elements del conjunt de destinació i tan sols rep informació dels elements concordants del conjunt d'elements a combinar, i per tant només pot resoldre relacions espacials 1:1 i M:1.
Els programes de SIG que segueixen una lògica més semblant a la dels sistemes de gestió de bases de dades, implementen la unió espacial com un nou conjunt de dades amb una taula d'atributs que conté la informació combinada dels registres de les taules d'atributs dels elements dels conjunts de dades de destinació i a combinar. En aquest tipus d'implementació sempre es genera un nou conjunt de dades com a resultat que s'emmagatzema físicament. D'aquesta manera és possible aplicar qualsevol dels tres tipus d'unió espacial (interna, esquerra i dreta) i resoldre també relacions espacials 1:M.
Algun dels programes de SIG que ha optat per aquesta implementació ofereix també l'opció de resoldre la unió espacial de relacions 1:M mitjançant la sumarització dels atributs quantitatius de la taula d'atributs del conjunt d'elements a combinar, que s'afegeixen a la taula d'atributs del conjunt d'elements de destinació en forma d'unió interna o d'unió esquerra, en lloc de fer la unió dreta.
El programari de gestió de bases de dades espacials no fa distinció entre unió relacional i unió espacial i simplement inclou els predicats espacials dins de les sentències de consulta, aplicant qualsevol tipus d'unió relacional segons que ho especifiqui l'usuari.
En el cas de la unió espacial és tant o més crític que en la unió relacional distingir entre el conjunt d'elements de destinació i el conjunt d'elements a combinar. No solament pel sentit de la unió de taules (esquerra o dreta), sinó també i especialment pel fet que les relacions espacials són diferents segons el sentit en què s'avaluïn.
Relacions espacials segons la geometria dels elements
Les relacions espacials habitualment utilitzades en els programes de SIG que implementen la unió espacial són intersecció, contenció, dins i element més proper:
- Intersecció: els elements del conjunt a combinar es fan correspondre amb els elements del conjunt de destinació que intersecten.
- Contenció: els elements del conjunt a combinar es fan correspondre amb els elements del conjunt de destinació que els contenen.
- Dins: els elements del conjunt a combinar es fan correspondre amb els elements del conjunt de destinació que són dins seu.
- Element més proper: els elements del conjunt a combinar es fan correspondre amb l'element més proper del conjunt de destinació. En cas que n'hi hagi més d'un a la mateixa distància se'n tria un aleatòriament.
Aquestes relacions espacials prenen sentit i cardinalitat diferent segons la geometria dels elements del conjunt de dades de destinació i la dels elements del conjunt de dades a combinar. Algunes, de fet, no són aplicables segons quina sigui la geometria d'un o altre dels conjunts de dades. La taula següent, resumeix les relacions espacials aplicables i el sentit que tenen per a cada combinació de tipus d'elements geomètrics de destinació i a combinar. Alguns programes, automatitzen aquesta definició de les relacions espacials i ofereixen només ´com a opcions d'usuari aquelles que són possibles en cada cas.
element de destinació | element a combinar | RELACIONS ESPACIALS | |||
intersecció | contenció | dins | més proper | ||
|
|
|
|
|
|
PUNTS: els punts adquireixen els atributs dels elements a combinar (punts, línies o polígons) | |||||
punt | punt | el punt a combinar correspon al punt de destinació que tingui la mateixa posició | el punt a combinar correspon al punt de destinació més proper | ||
punt | línia | la línia a combinar correspon al punt de destinació que estigui sobre la línia, inclosos els extrems |
| la línia a combinar correspon al punt de destinació que estigui sobre la línia, exclosos els extrems | la línia a combinar correspon al punt de destinació més proper |
punt | polígon | el polígon a combinar correspon al punt de destinació que estigui dins o sobre el contorn del polígon |
| el polígon a combinar correspon al punt de destinació que estigui dins del polígon, però no sobre el contorn | el polígon a combinar correspon al punt de destinació més proper |
|
|
|
|
|
|
LÍNIES: les línies adquireixen els atributs dels elements a combinar(punts, línies o polígons) | |||||
línia | punt | el punt a combinar correspon a la línia de destinació que el contingui, inclosos els extrems | el punt a combinar correspon a la línia de destinació que el contingui, exclosos els extrems |
| el punt a combinar correspon a la línia de destinació més propera |
línia | línia | la línia a combinar correspon a la línia de destinació amb què intersequi (creui, toqui o coincideixi totalment o parcial) | la línia a combinar correspon a la línia de destinació que la contingui totalment | la línia a combinar correspon a la línia de destinació que estigui completament dins de la línia a combinar | la línia a combinar correspon la línia de destinació més propera |
línia | polígon | el polígon a combinar correspon a la línia de destinació amb què intersequi |
| el polígon a combinar correspon a la linía de destinació que estigui dins del polígon, però no sobre el contorn | el polígon a combinar correspon a la línia de destinació més propera |
|
|
|
|
|
|
POLÍGONS: els polígons adquireixen els atributs dels elements a combinar(punts, línies o polígons) | |||||
polígon | punt | el punt a combinar correspon al polígon de destinació que el contingui, inclòs el contorn | el punt a combinar correspon al polígon de destinació que el contingui, exclòs el contorn |
| el punt a combinar correspon al polígon de destinació més proper |
polígon | línia | la línia a combinar correspon al polígon de destinació que la contingui amb què intersequi | la línia a combinar correspon al polígon de destinació que la contingui, exclòs el contorn |
| la línia a combinar correspon al polígon de destinació més proper |
polígon | polígon | el polígon a combinar correspon al polígon de destinació amb què intersequi | el polígon a combinar correspon al polígon de destinació que el contingui, exclòs el contorn | el polígon a combinar correspon a al polígon de destinació que estigui dins del polígon a combinar | el polígon a combinar correspon al polígon de destinació més proper |
Relacions espacials emprades a l'operació d'unió espacial, segons la geometria dels elements. |
En el cas de les bases de dades espacials que implementen els predicats espacials del model de nou interseccions estès dimensionalment, les relacions espacials que es poden utilitzar per a la unió espacial són igual (iquals), disjunt (disjoints), intersecció (intersect), toca (touches), creua (crosses), dins (within), conté (contains), cavalcament (overlaps), cobreix (covers) i cobert per (covered by).
La relació d'intersecció dels sistemes d’informació geogràfica comprèn sense diferenciar-les les relacions igual, intersecció, toca, creua i cavalcament. Disjunt, cobreix i cobert per són relacions addicionals possibles a les bases de dades espacials, mentre que la relació d'element més proper és una relació espacial addicional basada en la distància, emprada en els sistemes d’informació geogràfica.
Temes relacionats
- Base de dades espacial
- Model de nou interseccions estès dimensionalment
- Sistemes d’informació geogràfica
- Superposició
- Unió relacional
Referències
Aronson, P. (1987) "Attribute handling for geographic information systems" in Proceedings of AUTOCARTO 8. Falls Church, Virginia: ASPRS.
Clementini, E. and Di Felice, P. (1996) "Model for Representing Topological Relationships Between Complex Geometric Features", Spatial Databases.- Information Sciences, 90(1-4),121-136.
Laurini, R. and Thompson, D. (1992) Fundamentals of Spatial Information Systems, London: Academic Press.
Longley, P.A.; Goodchild, M.F.; Maguire, D.J. and Rhind, D.W. (eds.) (2010) Geographical Information Systems and Science, 3rd Edition. Hoboken, New Jersey: John Wiley & Sons.
Shekhar, S. and Chawla, S. (2003) Spatial Databases: A Tour, Upper Saddle River, New Jersey: Prentice Hall.
Lectures recomanades
Laurini, R. and Thompson, D. (1992) Fundamentals of Spatial Information Systems, London: Academic Press.

 Contacte
Contacte