Autor: Dr. Josep Maria Rabella. Universitat de Barcelona
Promotor: Institut Cartogràfic de Catalunya, 2013
sinònim: projecció
cs proyección cartográfica, proyección; fr projection, projection cartographique; it proiezione, proiezione cartografica; en map projection, projection; de Abbildung, kartographische Abbildung
SUMARI
Qualsevol sistema o mètode emprat per a transformar la representació cartogràfica de la superfície esferoïdal de la Terra a una superfície de referència plana.
Encara que el nombre de projeccions cartogràfiques possibles és pràcticament infinit, habitualment es treballa aproximadament amb un centenar d'elles. D'aquestes, només algunes són autènticament projeccions perspectives (i no per això sempre més útils), és a dir, resultat de projectar veritablement la superfície del globus per mètodes geomètrics o bé òptics. Malgrat això, per extensió, qualsevol mètode matemàtic o gràfic de transformació de l'esferoide al pla o, fins i tot, qualsevol configuració plana constituïda per una xarxa de línies que representin meridians i paral·lels com a xarxa de referència per al traçat de mapes, rep també aquesta denominació.
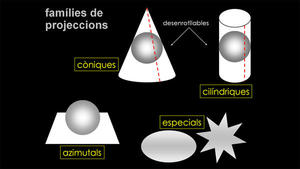
Classificació de les projeccions segons els seus principis constructius
Amb l'objectiu d'estudiar les nombroses projeccions d'una manera ordenada i sistemàtica, tradicionalment han estat classificades atenent al seu aspecte i tenint en compte, sobretot, els principis teòrics constructius que les inspira. Segons tot això, poden ser considerades les següents famílies o grups: projeccions cilíndriques, projeccions còniques, projeccions azimutals i projeccions especials.
Les projeccions cilíndriques i còniques es basen o s'inspiren en l'estratègia de projectar la superfície del globus sobre un cilindre o un con, respectivament, que posteriorment seran tallats per una generatriu i desenrotllats plans; per aquest motiu se les anomena, de vegades, projeccions desenrotllables. Les projeccions azimutals, en canvi, es basen o s'inspiren en la projecció directa del globus sobre una superfície ja plana. Finalment, moltes altres construccions que no s'inspiren en tals mètodes, ni s'associen ni s'assemblen a aquests esquemes, configuren l’extensa família que, com a "calaix de sastre", rep el nom genèric de projeccions especials.
La posició del globus
A més, dins de cada família i tipus, segons l'aspecte del mapa, i derivat de la inclinació que manté el globus respecte al cilindre, al con o al pla en el moment teòric de la transformació, la projecció resultant pot ser adjectivada com a directe o equatorial, transversa (o polar), o bé obliqua. Però en qualsevol cas, el simple canvi de la posició del globus no altera mai les propietats de cadascuna de les projeccions, malgrat que condicioni, lògicament, la disposició i l'aspecte de la seva imatge obtinguda.
Encara que aquesta classificació segons la descripció del seu origen o l'esquema que les inspira, presenta raons descriptives clares i ostenta valors didàctics acceptables, a més de ser la més popularitzada des del mateix ensenyament elemental, el seu enfocament resulta bastant irrellevant i, a voltes, fins i tot equívoc. En una aproximació més rigorosa i funcional és imprescindible atendre també, i sobretot, les qualitats dimensionals que manté cada projecció, a fi i efecte de seleccionar en cada ocasió i per a cada objectiu específic la més convenient.
El continuum conceptual entre el cilindre, el con i el pla
Independentment de les posicions del globus que només afecten l'aspecte purament formal de la imatge però no les propietats de la projecció, cal tenir present que, depenent de la configuració d'un con, més agut o tancat, o bé més pla i obert, la circumferència tangent o de contacte amb el globus (línia de referència o automecoica) variarà notablement de situació. En el cas extrem d'un con amb el vèrtex a l'infinit, aquest constituiria, en realitat, un cilindre i la circumferència tangent coincidiria amb un cercle màxim (l'equador, en la posició directa del globus), mentre que en l'altre extrem, el con quedaria convertit, en realitat, en un pla i la tangència es produiria en un determinat punt (un pol en la posició polar, per exemple). Això ens recorda un cop més que la popular classificació entre projeccions cilíndriques, còniques i azimutals és purament didàctica i descriptiva ja que, pròpiament, existeix una continuïtat teòrica i conceptual entre les tres famílies que, lògicament, se'n deriven les mateixes conseqüències matemàtiques i, en certa manera, faciliten el seu estudi en fer-les més simples.
Classificació de les projeccions cartogràfiques segons les seves qualitats topològiques o dimensionals
La impossibilitat real de traslladar informació cartogràfica des de l'esferoide al pla sense introduir alteracions dimensionals constitueix un problema ben conegut des de l'antiguitat, força desenvolupat en temps de la cultura clàssica grega i ja altament matematitzat a partir del segle XVIII. Però, si bé és cert que cap projecció cartogràfica no podrà mai aconseguir aplanar la superfície de la Terra sense produir deformacions o alteracions dimensionals, sí que esdevé possible estudiar i saber, en cada cas, quina alteració és generada i quina pot resultar evitable, és a dir, quina qualitat o característica dimensional resta en cada projecció, informació que aporta la dada més útil i rellevant del tema.
Les projeccions conformes són les que mantenen constants els valors angulars sobre punts (òbviament, no entre punts distants) i, en canvi, modifiquen i falsegen les magnituds de superfície de les àrees representades, impossibilitant-ne les comparacions. La seva utilitat és aprofitada especialment en la confecció de cartes per a la navegació, sobre les que cal mesurar angles i rumbs.
Les projeccions equivalents mantenen proporcionals, en canvi, les magnituds superficials de les àrees representades, però ho fan pagant el preu d'alterar els valors angulars i produir biaixos. La seva qualitat les fa favorables, és clar, per a representar densitats o comparar superfícies territorials.
Convé remarcar en aquest punt que cap projecció no pot ser mai a la vegada conforme i equivalent, ja que aquestes propietats resulten, no només totalment incompatibles sinó, també, contradictòries matemàticament parlant.
Les projeccions equidistants són les que mantenen les distàncies proporcionals (amb escala constant) respecte a les del territori, però això només pot esdevenir possible en determinades i molt limitades direccions (que poden ser conegudes), mai en totes. Temes zonals de climatologia, distàncies des d'aeroports o estudis de cobertures o abast d'antenes poden ser ben plasmats en mapes d'aquestes especials característiques.
La projecció gnomònica és l'única, entre totes les possibles, que permet traçar els itineraris més curts entre dos punts qualsevol de la superfície del globus (arcs de cercles màxims) en forma de segments rectilinis sobre els mapes plans obtinguts amb ella (exclusivament amb ella) que és el que intuïtivament tothom interpretaria com a "camí més curt". Els llargs trajectes en vaixell o avió són determinats, doncs, de forma ben simple sobre aquestes cartes.
Les projeccions afilàctiques són les que, sense mantenir pròpiament cap de les qualitats anteriorment esmentades, aconsegueixen una certa solució de compromís entre unes i altres, compensant fins un cert punt la falta d'exactitud en cada variable dimensional, oferint així una percepció de conjunt acceptable per a usos informatius generals o purament d'imatge de conjunt. Multitud de planisferis de despatx i de mapamundis murals i d'atles, didàctics i per a usos generals, per exemple, es basen en aquest tipus de projecció.
Temes relacionats
- cartografia
- mapa
- projecció afilàctica
- projecció azimutal
- projecció cilíndrica
- projecció conforme
- projecció cònica
- projecció especial
- projecció equidistant
- projecció equivalent
- xarxa geogràfica
Referències
BOENA RUIZ, Julián i altres: La esfera. Madrid, Editorial Síntesis, 1996. ISBN: 84-7738-356-1
ROBINSON, A. H. i SNYDER, J. P. (ed.): Matching the Map Projeccion to the Need. American Congress on Surveying and Mapping, 1991. ISBN: 0-9613459-5-0
SNYDER, John P.: Flattening the Earth. Two Thousand Years of Map Projections. Chicago, Londres, The University of Chicago Press, 1993.ISNB 0-226-76746-9.
STRAHLER, Arthut N. i STRAHLER, Alan H.: Modern Physical Geography. Nova York, John Wiley & Sons, 1987 (3a). En castellà: Geografía física. Omega, 1989.
Lectures recomanades
MONMONIER, Mark S.: Maps, Distorsion, and Meaning. Washington, Association of American Geographers, 1989. ISBN 0-89291-120-4.
RABELLA i VIVES, Josep M.: “Mil projeccions per a un mapamundi”, a Revista Catalana de Geografia,núm 11. Barcelona,Institut Cartogràfic de Catalunya, 1990. ISSN 0210-6000.

 Contacte
Contacte